
分析 (Ⅰ)首先,根据二倍角公式和辅助角公式,得到该函数的解析式f(x)=2sin(2x+$\frac{π}{4}$),然后,确定其周期和单调递增区间;
(Ⅱ)结合(Ⅰ)和所给自变量的范围,根据正弦函数的单调性进行确定其最小值.
解答 解:(Ⅰ)∵f(x)=sin2x+2cos2x-1.
=sin2x+cos2x
=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
∴f(x)=2sin(2x+$\frac{π}{4}$)
∴该函数的周期为:T=$\frac{2π}{2}$=π.
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z,
∴-$\frac{3π}{8}$+kπ≤x≤$\frac{π}{8}$+kπ,k∈Z,
∴单调递增区间:[-$\frac{3π}{8}$+kπ,$\frac{π}{8}$+kπ],(k∈Z).
(Ⅱ)根据(Ⅰ),知
f(x)=2sin(2x+$\frac{π}{4}$),
∵$\frac{π}{4}$≤x≤$\frac{3π}{4}$,
∴$\frac{3π}{4}$≤2x+$\frac{π}{4}$≤$\frac{7π}{4}$,
∴当2x+$\frac{π}{4}$=$\frac{3π}{2}$时,即x=$\frac{5π}{8}$时,该函数有最小值为-$\sqrt{2}$.
点评 本题重点考查了二倍角公式、辅助角公式、三角函数的单调性与最值等知识,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {α|90°<α<180°} | B. | {α|180°<α<270°} | ||
| C. | {α|90°+k•360°<α<180°+k•360°,k∈Z} | D. | {α|180°+k•360°<α<270°+k•360°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
已知等比数列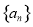 ,各项
,各项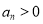 ,公比为
,公比为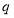 .(1)设
.(1)设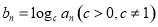 ,求证:
,求证:
(1)数列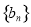 是等差数列,并求出该数列的首项
是等差数列,并求出该数列的首项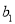 及公差
及公差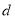 ;
;
(2)设(1)中的数列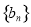 单调递减,求公比
单调递减,求公比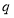 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:选择题
已知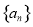 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是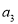 与
与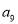 的等比中项,
的等比中项,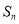 为
为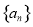 的前
的前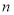 项和,则
项和,则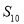 的值为( )
的值为( )
A.-110 B.-90 C.90 D.110
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.
从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com