
剖析:解本题的关键是按题意画出相应的空间图形,将点(飞机)到水平面的距离,转化到水平面上,利用平面几何知识求解.
解:如图,A、C分别是汽车、飞机开始的位置,B、D分别是经过36秒后的位置,ABEF是水平面,CFED是矩形,且CD=![]() ×100
×100![]() =
=![]() (千米),AB=
(千米),AB=![]() ×100=1(千米),CF(或DE)则为飞机飞行的高度,设其为x千米,在Rt△CFA中,AF=
×100=1(千米),CF(或DE)则为飞机飞行的高度,设其为x千米,在Rt△CFA中,AF=![]() x;在Rt△DEB中,BE=
x;在Rt△DEB中,BE=![]() x.
x.

作EG⊥AB于G,EH⊥AF于H,则EG=AH=![]() x,
x,
EH=AG=AB+BG=1+![]() x,FH=
x,FH=![]() x.
x.
在Rt△FHE中,EF2=FH2+EH2,即(![]() )2=(
)2=(![]() x)2+(1+
x)2+(1+![]() x)2,
x)2,
∴x=1.
故飞机飞行的高度为1千米.
讲评:这是一道立体几何应用题,认识现实生活中常接触的一些概念:仰角、俯角、方位角、方向角等.应用时确定它们在图形中的位置是关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
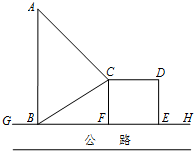 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,设AB=y km,并在公路同侧建造边长为x km的正方形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°.
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,设AB=y km,并在公路同侧建造边长为x km的正方形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
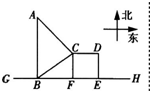 如图所示,GH是一条东西方向的公路,现准备在点B的正北方向的点A处建一仓库,设AB=y千米,并在公路旁边建造边长为x千米的正方形无顶中转站CDEF(其中边EF在公路GH上),现向公路和中转站分别修两条简易公路AB,AC,已知AB=AC+1,且∠ABC=60°.
如图所示,GH是一条东西方向的公路,现准备在点B的正北方向的点A处建一仓库,设AB=y千米,并在公路旁边建造边长为x千米的正方形无顶中转站CDEF(其中边EF在公路GH上),现向公路和中转站分别修两条简易公路AB,AC,已知AB=AC+1,且∠ABC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:
如图某粮食储备库占地呈圆域形状,它的斜对面有一条公路,从储备库中心A向正东方向走1km是储备库边界上的点B,接着向正东方向再走2km到达公路上的点C;从A向正北方向走2.8km到达公路上的另一点D,现准备在储备库的边界上选一点E,修建一条由E通往公路CD的专用(线)路EF,要求EF最短,问点E应选在何处?
 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com