
分析 设P(2$\sqrt{2}$cosθ,m+2$\sqrt{2}$sinθ),由P到直线l:x+y-3=0的距离为3$\sqrt{2}$,得$|4sin(θ+\frac{π}{4})-3+m|$=6,由此利用三角函数性质能求出实数m的取值范围.
解答 解:∵圆M:x2+(y-m)2=8,圆M上存在点P,
∴设P(2$\sqrt{2}$cosθ,m+2$\sqrt{2}$sinθ),
∵P到直线l:x+y-3=0的距离为3$\sqrt{2}$,
∴$\frac{|2\sqrt{2}cosθ+m+2\sqrt{2}sinθ-3|}{\sqrt{2}}$=3$\sqrt{2}$,
即$|4sin(θ+\frac{π}{4})-3+m|$=6,
∵$-7≤4sin(θ+\frac{π}{4}-3)+m≤1$,
∴-7≤m≤1或5≤m≤13,
∴实数m的取值范围是[-7,1]∪[5,13].
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意点到直线距离公式和三角函数性质的合理运用.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1]∪(0,1] | B. | (-∞,-1]∪[0,1] | C. | (0,1] | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,5,7} | B. | {1,5,7} | C. | {1,3,9} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\sqrt{10}$ | D. | $\frac{2\sqrt{390}}{39}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
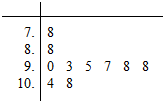 某射击爱好者想提高自己的射击水平,制订了了一个训练计划,为了了解训练效果,执行训练计划前射击了10发子弹(每发满分为10.9环),计算出成绩中位数为9.65环,总成绩为95.1环,成绩标准差为1.09环,执行训练计划后也射击了10发子弹,射击成绩茎叶图如图所示.
某射击爱好者想提高自己的射击水平,制订了了一个训练计划,为了了解训练效果,执行训练计划前射击了10发子弹(每发满分为10.9环),计算出成绩中位数为9.65环,总成绩为95.1环,成绩标准差为1.09环,执行训练计划后也射击了10发子弹,射击成绩茎叶图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com