
分析 (1)利用f(0)=f2(0),f(0)≠0,求f(0)的值;
(2)f(x)=f($\frac{x}{2}$+$\frac{x}{2}$)=f2($\frac{x}{2}$),结合函数f(x)为非零函数可得;
(3)证明f(x)为减函数,由f(4)=f2(2)=$\frac{1}{16}$,则f(2)=$\frac{1}{4}$,从而化简不等式f(x-3)•f(5-x2)≤$\frac{1}{4}$为f(x-3+5-x2)≤f(2),从而利用单调性求解.
解答 (1)解:∵f(0)=f2(0),f(0)≠0,∴f(0)=1,
(2)证明:∵f($\frac{x}{2}$)≠0,
∴f(x)=f($\frac{x}{2}$+$\frac{x}{2}$)=f2($\frac{x}{2}$)>0.
(3)解:f(b-b)=f(b)•f(-b)=1;
∴f(-b)=$\frac{1}{f(b)}$;
任取x1<x2,则x1-x2<0,
∴$\frac{f({x}_{1})}{f({x}_{2})}$=f(x1-x2)>1,
又∵f(x)>0恒成立,
∴f(x1)>f(x2),∴f(x)为减函数;
由f(4)=f2(2)=$\frac{1}{16}$,则f(2)=$\frac{1}{4}$,
原不等式转化为f(x-3+5-x2)≤f(2),
结合(2)得:x+2-x2≥2,
∴0≤x≤1,
故不等式的解集为{x|0≤x≤1}.
点评 本题考查了函数单调性的证明与应用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
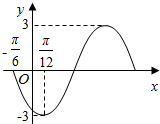 函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的部分图象如图所示,则其解析式是y=3sin(2x-$\frac{2π}{3}$).
函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的部分图象如图所示,则其解析式是y=3sin(2x-$\frac{2π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
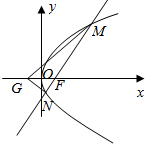 已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2
已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com