
【题目】将函数f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1的图象向左平移
cos2x+1的图象向左平移 ![]() 个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
A.函数y=g(x)的最小正周期为π
B.函数y=g(x)的图象的一条对称轴为直线x= ![]()
C.![]() g(x)dx=
g(x)dx= ![]()
D.函数y=g(x)在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
【答案】D
【解析】解:把f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1=2sin(2x﹣
cos2x+1=2sin(2x﹣ ![]() )+1的图象向左平移
)+1的图象向左平移 ![]() 个单位, 得到函数y=2sin[2(x+
个单位, 得到函数y=2sin[2(x+ ![]() )﹣
)﹣ ![]() ]+1=2sin(2x+
]+1=2sin(2x+ ![]() )+1的图象,
)+1的图象,
再向下平移1个单位,得到函数y=g(x)=2sin(2x+ ![]() )的图象,
)的图象,
对于A,由于T= ![]() ,故正确;
,故正确;
对于B,由2x+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,解得:x=
,k∈Z,解得:x= ![]() +
+ ![]() ,k∈Z,可得:当k=0时,y=g(x)的图象的一条对称轴为直线x=
,k∈Z,可得:当k=0时,y=g(x)的图象的一条对称轴为直线x= ![]() ,故正确;
,故正确;
对于C, ![]() g(x)dx=
g(x)dx= ![]() 2sin(2x+
2sin(2x+ ![]() )dx=﹣cos(2x+
)dx=﹣cos(2x+ ![]() )|
)| ![]() =﹣(cos
=﹣(cos ![]() ﹣cos
﹣cos ![]() )=
)= ![]() ,故正确;
,故正确;
对于D,由2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,解得:kπ+
,k∈Z,解得:kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,可得函数y=g(x)在区间[
,k∈Z,可得函数y=g(x)在区间[ ![]() ,
, ![]() ]上单调递减,故错误.
]上单调递减,故错误.
故选:D.
利用两角差的正弦函数公式、函数y=Asin(ωx+φ)的图象变换规律,可得g(x),利用正弦函数的图象和性质逐一分析各个选项即可得解.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.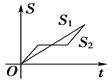 B.
B.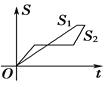 C.
C.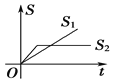 D.
D.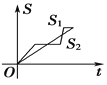
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,椭圆C的参数方程为 ![]() (θ为参数).
(θ为参数).
(1)以原点为极点,x轴的正半轴为极轴建立极坐标系,求椭圆C的极坐标方程;
(2)设M(x,y)为椭圆C上任意一点,求x+2y的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大报告指出,建设生态文明是中华民族永续发展的千年大计.而清洁能源的广泛使用将为生态文明建设提供更有力的支撑.沼气作为取之不尽、用之不竭的生物清洁能源,在保护绿水青山方面具有独特功效.通过办沼气带来的农村“厕所革命”,对改善农村人居环境等方面,起到立竿见影的效果.为了积极响应国家推行的“厕所革命”,某农户准备建造一个深为2米,容积为32立方米的长方体沼气池,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,沼气池盖子的造价为3000元,问怎样设计沼气池能使总造价最低?最低总造价是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算机在数据处理时使用的是二进制,例如十进制的1、2、3、4在二进制分别表示为1、10、11、100.下面是某同学设计的将二进制数11111化为十进制数的一个流程图,则判断框内应填入的条件是( ) 
A.i>4
B.i≤4
C.i>5
D.i≤5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com