
【题目】设不等式组  所表示的平面区域为Dn , 记Dn内的整点个数为an(n∈N*).(整点即横坐标和纵坐标均为整数的点)
所表示的平面区域为Dn , 记Dn内的整点个数为an(n∈N*).(整点即横坐标和纵坐标均为整数的点)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列{an}的前n项和为Sn , 且 ![]() ,若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
,若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
【答案】解:(I)由x>0,y>0,3n﹣nx>0,得0<x<3,∴x=1或x=2, ∴Dn内的整点在直线x=1和x=2上,记直线y=﹣nx+3n为l,l与直线x=1,x=2的交点的纵坐标分别为y1、y2 ,
则y1=﹣n+3n=2n,y2=﹣2n+3n=n,
∴ ![]() ;
;
(II)∵ ![]() ,
,
∴当n≥3时,Tn>Tn+1 , 且 ![]() ,
,
∴T2 , T3是数列{Tn}中的最大项,故 ![]()
【解析】(Ⅰ)由x>0,y>0,3n﹣nx>0,可求得x=1,或x=2,则Dn内的整点在直线x=1和x=2上,联立可求得整点纵坐标,进而可得整点个数;(Ⅱ)先求出Sn , 从而可得Tn , 通过作差可求得Tn的最大项,则m大于等于最大项;
【考点精析】通过灵活运用二元一次不等式(组)所表示的平面区域,掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且经过点(1,
,且经过点(1, ![]() ),F1 , F2是椭圆的左、右焦点.
),F1 , F2是椭圆的左、右焦点.
(1)求椭圆C的方程;
(2)点P在椭圆上运动,求|PF1||PF2|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线l1:ax﹣y+a=0,l2:x+ay﹣a(a+1)=0,l3:(a+1)x﹣y+a+1=0,a>0.
(1)证明:这三条直线共有三个不同的交点;
(2)求这三条直线围成的三角形的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x,第二次出现的点数为y.
(1)求事件“x+y≤3”的概率;
(2)求事件“|x﹣y|=2”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过不重合的A(m2+2,m2﹣3),B(3﹣m﹣m2 , 2m)两点的直线l倾斜角为45°,则m的取值为( )
A.m=﹣1
B.m=﹣2
C.m=﹣1或2
D.m=l或m=﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且 ![]() =
= ![]() ,a1=m,现有如下说法: ①a2=5;
,a1=m,现有如下说法: ①a2=5;
②当n为奇数时,an=3n+m﹣3;
③a2+a4+…+a2n=3n2+2n.
则上述说法正确的个数为( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为 . 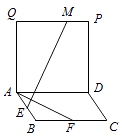
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com