
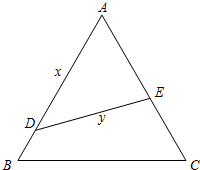
 如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE方便花园管理.设D、E分别在AB、AC上,且DE均分三角形ABC的面积.
如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE方便花园管理.设D、E分别在AB、AC上,且DE均分三角形ABC的面积.| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2a2 |
| x |
x2+
|
|
x2+
|
t+
|
| 4a4 |
| t |
| (t1-t2)(t1t2-4a4) |
| t1t2 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
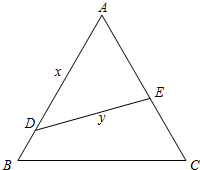 如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE方便花园管理.设D、E分别在AB、AC上,且DE均分三角形ABC的面积.
如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE方便花园管理.设D、E分别在AB、AC上,且DE均分三角形ABC的面积.查看答案和解析>>
科目:高中数学 来源:2009-2010学年人教A版高二期末调研数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)
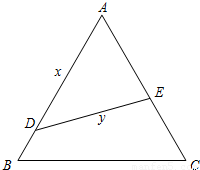
如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE
方便花园管理. 设D、E分别在AB、AC上,且DE均分三角形ABC的面积.
 (1)设AD=x(
(1)设AD=x(![]() ),DE=y,试将y表示为x的函数关系式;
),DE=y,试将y表示为x的函数关系式;
(2)若DE是灌溉水管,为节约成本,希望其最短,DE的位置应在哪里?
若DE是参观路线,希望其最长,DE的位置应在哪里?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)
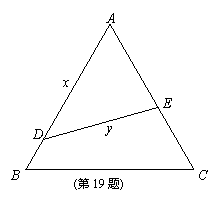
如图,公园内有一块边长为2a的正三角形ABC空地,拟改建成花园,并在其中建一直道DE
方便花园管理. 设D、E分别在AB、AC上,且DE均分三角形ABC的面积.
 (1)设AD=x(
(1)设AD=x(![]() ),DE=y,试将y表示为x的函数关系式;
),DE=y,试将y表示为x的函数关系式;
(2)若DE是灌溉水管,为节约成本,希望其最短,DE的位置应在哪里?
若DE是参观路线,希望其最长,DE的位置应在哪里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com