
【题目】设![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,在
时,在![]() 内是否存在一实数
内是否存在一实数![]() ,使
,使![]() 成立?请说明理由.
成立?请说明理由.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为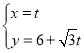 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日迎来了我国建党98周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为( )
A.20.5B.21元C.21.5元D.22元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,焦距为2,抛物线
,焦距为2,抛物线![]() 的准线经过
的准线经过![]() 的左焦点
的左焦点![]() .
.
(1)求![]() 与
与![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的上顶点且
的上顶点且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与
与![]() 分别交于点
分别交于点![]() (异于点
(异于点![]() ),
),![]() (异于点
(异于点![]() ),证明:直线
),证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(2+x)+lg(2﹣x).
(1)求函数f(x)的定义域并判断函数f(x)的奇偶性;
(2)记函数g(x)=![]() +3x,求函数g(x)的值域;
+3x,求函数g(x)的值域;
(3)若不等式 f(x)>m有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 地正西方向
地正西方向![]() 的
的![]() 处和正东方向
处和正东方向![]() 的
的![]() 处各一条正北方向的公路
处各一条正北方向的公路![]() 和
和![]() ,现计划在
,现计划在![]() 和
和![]() 路边各修建一个物流中心
路边各修建一个物流中心![]() 和
和![]() .
.
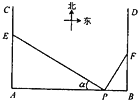
(1)若在![]() 处看
处看![]() ,
,![]() 的视角
的视角![]() ,在
,在![]() 处看
处看![]() 测得
测得![]() ,求
,求![]() ,
,![]() ;
;
(2)为缓解交通压力,决定修建两条互相垂直的公路![]() 和
和![]() ,设
,设![]() ,公路
,公路![]() 的每千米建设成本为
的每千米建设成本为![]() 万元,公路
万元,公路![]() 的每千米建设成本为
的每千米建设成本为![]() 万元.为节省建设成本,试确定
万元.为节省建设成本,试确定![]() ,
,![]() 的位置,使公路的总建设成本最小.
的位置,使公路的总建设成本最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com