
【题目】某电影院共有![]() 个座位.某天,这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生,三所学校的观影人数分别是985人, 1010人,2019人(同一所学校的学生有的看上午场,也有的看下午场,但每人只能看一-场).已知无论如何排座位,这天观影时总存在这样的一个座位,上、 下午在这个座位上坐的是同一所学校的学生,那么
个座位.某天,这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生,三所学校的观影人数分别是985人, 1010人,2019人(同一所学校的学生有的看上午场,也有的看下午场,但每人只能看一-场).已知无论如何排座位,这天观影时总存在这样的一个座位,上、 下午在这个座位上坐的是同一所学校的学生,那么![]() 的可能取值有( )
的可能取值有( )
A. 12个 B. 11个 C. 10个 D. 前三个答案都不对
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x﹣ ![]() )+cos(x﹣
)+cos(x﹣ ![]() ),g(x)=2sin2
),g(x)=2sin2 ![]() .
.
(1)若α是第一象限角,且f(α)= ![]() ,求g(α)的值;
,求g(α)的值;
(2)求使f(x)≥g(x)成立的x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点. 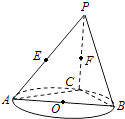
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足 ![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 
(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是()
A. 锐角是第一象限的角,所以第一象限的角都是锐角;
B. 如果向量![]() ,则
,则![]() ;
;
C. 在![]() 中,记
中,记![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 可以作为平面ABC内的一组基底;
可以作为平面ABC内的一组基底;
D. 若![]() ,
,![]() 都是单位向量,则
都是单位向量,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比为q,记bn=am(n﹣1)+1+am(n﹣1)+2+…+am(n﹣1)+m , cn=am(n﹣1)+1am(n﹣1)+2…am(n﹣1)+m , (m,n∈N*),则以下结论一定正确的是( )
A.数列{bn}为等差数列,公差为qm
B.数列{bn}为等比数列,公比为q2m
C.数列{cn}为等比数列,公比为 ![]()
D.数列{cn}为等比数列,公比为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com