
【题目】已知函数f(x)的定义域为R,对任意的实数x,y都有f(x+y)=f(x)+f(y)+ ![]() ,且f(
,且f( ![]() )=0,当x>
)=0,当x> ![]() 时,f(x)>0.
时,f(x)>0.
(1)求f(1);
(2)判断函数f(x)的单调性,并证明.
【答案】
(1)解:由对任意的实数x,y都有f(x+y)=f(x)+f(y)+ ![]() ,且f(
,且f( ![]() )=0,
)=0,
令y=x= ![]() ,得f(1)=f(
,得f(1)=f( ![]() )+f(
)+f( ![]() )+
)+ ![]() =
= ![]()
(2)解:设x>0 则x+ ![]() .
.
∴ ![]() .
.
即f(x)>﹣ ![]() ,
,
任取x1,x2∈(﹣∞,+∞),且x1>x2
则x1﹣x2>0
∴f(x1)=f[(x1﹣x2)+x2]=f(x1﹣x2)+f(x2)+ ![]() >f(x2)
>f(x2)
∴f(x)在(﹣∞,+∞)上为增函数
【解析】(1)利用赋值法,令y=x= ![]() 即可求得f(1)的值;(2)由当x>
即可求得f(1)的值;(2)由当x> ![]() 时,f(x)>0,结合给出的等式得到当x>0时,f(x)>﹣
时,f(x)>0,结合给出的等式得到当x>0时,f(x)>﹣ ![]() ,然后利用函数单调性定义,借助于题目给出的等式判断.
,然后利用函数单调性定义,借助于题目给出的等式判断.
【考点精析】关于本题考查的函数单调性的判断方法,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能得出正确答案.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象
在某一个周期内的图象
时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解
的解
析式;
(Ⅱ)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]()
![]() 个单位长度,得到
个单位长度,得到![]() 的图
的图
象. 若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,判断条件p是条件q的什么条件:
(1)p:|x|=|y|,q:x=y;
(2)p:△ABC是直角三角形,q:△ABC是等腰三角形;
(3)p:四边形的对角线互相平分,q:四边形是矩形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区2017年上半年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
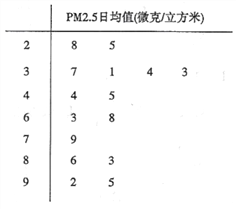
(1)从这15天的数据中任取一天,求这天空气质量达到一级的概率;
(2)从这15天的数据中任取3天的数据,记![]() 表示其中空气质量达到一级的天数,求
表示其中空气质量达到一级的天数,求![]() 的分布列;
的分布列;
(3)以这15天的PM2.5的日均值来估计一年的空气质量情况,(一年按360天来计算),则一年中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A.?![]() ∈R,使sin(
∈R,使sin(![]() )=
)=![]() +sinβ
+sinβ
B.?![]() ∈R,函数f(x)=sin(
∈R,函数f(x)=sin(![]() )都不是偶函数
)都不是偶函数
C.?m∈R,使f(x)=(m-1)·m2-4m+3是幂函数,且在(0,+∞)上单调递减
D.?![]() >0,函数f(x)=ln2x+lnx-
>0,函数f(x)=ln2x+lnx-![]() 有零点
有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的 ![]() ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com