
【题目】双十一购物狂欢节,是指每年11月11日的网络促销日,源于淘宝商城(天猫)2009年11月11日举办的网络促销活动,已成为中国电子商务行业的年度盛事.某生产商为了了解其生产的产品在不同电商平台的销售情况,统计了![]() 两个电商平台各十个网络销售店铺的销售数据:
两个电商平台各十个网络销售店铺的销售数据:
| 64 | 71 | 81 | 70 | 79 | 69 | 82 | 73 | 75 | 60 |
| 60 | 80 | 97 | 77 | 96 | 87 | 76 | 83 | 94 | 96 |
(1)作出![]() 两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
(2)填写下面关于店铺个数的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为销售量与电商平台有关;
的把握认为销售量与电商平台有关;
销售量 | 销售量 | 总计 | |
| |||
| |||
总计 |
(3)生产商要从这20个网络销售店铺销售量前五名的店铺中,随机抽取三个店铺进行销售返利,则其中恰好有两个店铺的销售量在95以上的概率是多少?
附: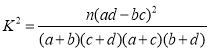 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)茎叶图见解析,![]() 电商平台的销售更好,理由见解析(2)
电商平台的销售更好,理由见解析(2)![]() 列联表答案见解析,没有
列联表答案见解析,没有![]() 的把握认为销售量与电商平台有关. (3)
的把握认为销售量与电商平台有关. (3)![]()
【解析】
(1)由已知数据作出茎叶图,由茎叶图可知,![]() 电商、
电商、![]() 电商平台销售量的中位数及平均数,可得
电商平台销售量的中位数及平均数,可得![]() 电商平台的销售更好;
电商平台的销售更好;
(2)由题中数据,可将![]() 列联表补充完整,数据代入公式可得
列联表补充完整,数据代入公式可得![]() ,故没有
,故没有![]() 的把握认为销售量与电商平台有关;
的把握认为销售量与电商平台有关;
(3)由已知数据,从销售量前五名的店铺选取三个店铺共有10种情况,其中恰好有两个店铺的销售量在95以上的情况有6种,由古典概型求概率可得.
(1)由已知数据作出茎叶图如下:
A电商平台 | B电商平台 | ||||||||||
9 | 4 | 0 | 6 | 0 | |||||||
9 | 5 | 3 | 1 | 0 | 7 | 6 | 7 | ||||
2 | 1 | 8 | 0 | 3 | 7 | ||||||
9 | 4 | 6 | 6 | 7 | |||||||
由茎叶图可知:![]() 电商平台的销售更好,理由如下:
电商平台的销售更好,理由如下:
①由茎叶图可知,![]() 电商平台销售量的中位数为72,
电商平台销售量的中位数为72,![]() 电商平台销售量的中位数为85,因此
电商平台销售量的中位数为85,因此![]() 电商平台的销售更好.
电商平台的销售更好.
②由茎叶图可求得![]() 电商平台销售量的平均数为72.4,
电商平台销售量的平均数为72.4,![]() 电商平台销售量的平均数为84.6,因此
电商平台销售量的平均数为84.6,因此![]() 电商平台的销售更好.
电商平台的销售更好.
(2)由题中数据,可得![]() 列联表如下:
列联表如下:
销售量 | 销售量 | 总计 | |
| 2 | 8 | 10 |
| 6 | 4 | 10 |
总计 | 8 | 12 | 20 |
![]() ,
,
![]() 没有
没有![]() 的把握认为销售量与电商平台有关.
的把握认为销售量与电商平台有关.
(3)由已知数据,销售量前五名的店铺,销售量分别为97,96,96,94,87.
设对应的店铺分别为![]() .
.
从其中选取三个店铺共有10种情况,如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
其中恰好有两个店铺的销售量在95以上的情况有6种:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 其中恰好有两个店铺的销售量在95以上的概率
其中恰好有两个店铺的销售量在95以上的概率![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
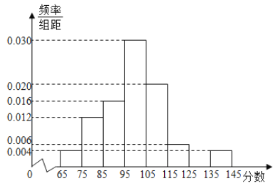
(1)求第七组的频率;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(I)写出直线![]() 的一般方程与曲线
的一般方程与曲线![]() 的直角坐标方程,并判断它们的位置关系;
的直角坐标方程,并判断它们的位置关系;
(II)将曲线![]() 向左平移
向左平移![]() 个单位长度,向上平移
个单位长度,向上平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]() ,设曲线
,设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线斜率为0.函数
处的切线斜率为0.函数![]()
(1)试用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)求![]() 的单调区间;
的单调区间;
(3)令![]() ,设函数
,设函数![]() 在
在![]()
![]() 处取得极值,记点
处取得极值,记点![]() ,
,![]() ,证明:线段
,证明:线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() ,
,![]() 的公共点.
的公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将斜边长为![]() 的等腰直角
的等腰直角![]() 沿斜边
沿斜边![]() 上的高
上的高![]() 折成直二面角
折成直二面角![]() ,
,![]() 为
为![]() 中点.
中点.
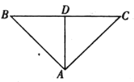
(1)求二面角![]() 的余弦值;
的余弦值;
(2)![]() 为线段
为线段![]() 上一动点,当直线
上一动点,当直线![]() 与平面
与平面![]() 所成的角最大时,求三棱锥
所成的角最大时,求三棱锥![]() 外接球的体积.
外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】鱼卷是泉州十大名小吃之一,不但本地人喜欢,而且深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户当地的习俗是农历正月不生产鱼卷,客户正月所需要的鱼卷都会在上一年农历十二月底进行一次性采购小张把去年年底采购鱼卷的数量x(单位:箱)在![]() 的客户称为“熟客”,并把他们去年采购的数量制成下表:
的客户称为“熟客”,并把他们去年采购的数量制成下表:
采购数x |
|
|
|
|
|
客户数 | 10 | 10 | 5 | 20 | 5 |
(1)根据表中的数据作出频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;
(2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的![]() ,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
(3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若不在网上出售鱼卷,则按去年的价格出售,每箱利润为20元,预计销售量与去年持平;若在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元(![]() )销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
)销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
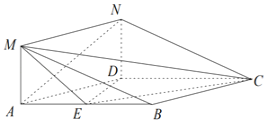
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上的动点,二面角
上的动点,二面角![]() 的平面角的大小为30°,求线段
的平面角的大小为30°,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为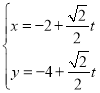 (t为参数),以坐标原点O为极点,以x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)已知定点![]() ,直线
,直线![]() 与曲线C分别交于P、Q两点,求
与曲线C分别交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com