
【题目】已知函数f(x)=lnx+x2 .
(1)若函数g(x)=f(x)﹣ax在其定义域内为增函数,求实数a的取值范围;
(2)在(1)的条件下,若a>1,h(x)=e3x﹣3aexx∈[0,ln2],求h(x)的极小值;
(3)设F(x)=2f(x)﹣3x2﹣kx(k∈R),若函数F(x)存在两个零点m,n(0<m<n),且2x0=m+n.问:函数F(x)在点(x0 , F(x0))处的切线能否平行于x轴?若能,求出该切线方程;若不能,请说明理由.
【答案】
(1)解:g(x)=f(x)﹣ax=lnx+x2﹣ax, ![]()
由题意知,g′(x)≥0,对任意的x∈(0,+∞)恒成立,即 ![]()
又∵x>0, ![]() ,当且仅当
,当且仅当 ![]() 时等号成立
时等号成立
∴ ![]() ,可得
,可得 ![]()
(2)解:由(1)知, ![]() ,令t=ex,则t∈[1,2],则
,令t=ex,则t∈[1,2],则
h(t)=t3﹣3at, ![]()
由h′(t)=0,得 ![]() 或
或 ![]() (舍去),
(舍去),
∵ ![]() ,∴
,∴ ![]()
若 ![]() ,则h′(t)<0,h(t)单调递减;若
,则h′(t)<0,h(t)单调递减;若 ![]() ,则h′(t)>0,h(t)单调递增
,则h′(t)>0,h(t)单调递增
∴当 ![]() 时,h(t)取得极小值,极小值为
时,h(t)取得极小值,极小值为 ![]()
(3)解:设F(x)在(x0,F(x0))的切线平行于x轴,其中F(x)=2lnx﹣x2﹣kx
结合题意,有 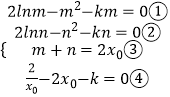
①﹣②得 ![]()
所以 ![]() ,由④得
,由④得 ![]()
所以 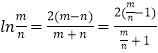 ⑤
⑤
设 ![]() ,⑤式变为
,⑤式变为 ![]()
设 ![]() ,
, ![]()
所以函数 ![]() 在(0,1)上单调递增,
在(0,1)上单调递增,
因此,y<y|u=1=0,即 ![]() ,也就是
,也就是 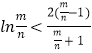 此式与⑤矛盾
此式与⑤矛盾
所以F(x)在(x0,F(x0))的切线不能平行于x轴
【解析】(1)先根据题意写出:g(x)再求导数,由题意知,g′(x)≥0,x∈(0,+∞)恒成立,即 ![]() 由此即可求得实数a的取值范围;(2)由(1)知
由此即可求得实数a的取值范围;(2)由(1)知 ![]() ,利用换元法令t=ex , 则t∈[1,2],则h(t)=t3﹣3at,接下来利用导数研究此函数的单调性,从而得出h(x)的极小值;(3)对于能否问题,可先假设能,即设F(x)在(x0 , F(x0))的切线平行于x轴,其中F(x)=2lnx﹣x2﹣kx结合题意,列出方程组,证得函数
,利用换元法令t=ex , 则t∈[1,2],则h(t)=t3﹣3at,接下来利用导数研究此函数的单调性,从而得出h(x)的极小值;(3)对于能否问题,可先假设能,即设F(x)在(x0 , F(x0))的切线平行于x轴,其中F(x)=2lnx﹣x2﹣kx结合题意,列出方程组,证得函数 ![]() 在(0,1)上单调递增,最后出现矛盾,说明假设不成立,即切线不能否平行于x轴.
在(0,1)上单调递增,最后出现矛盾,说明假设不成立,即切线不能否平行于x轴.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= ![]() PD.
PD.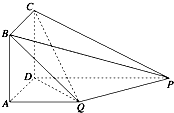
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q﹣BP﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有1 000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数见右上表,据此估计这1 000根中纤维长度不小于37.5 mm的根数是 .
纤维长度 | 频数 |
[22.5,25.5) | 3 |
[25.5,28.5) | 8 |
[28.5,31.5) | 9 |
[31.5,34.5) | 11 |
[34.5,37.5) | 10 |
[37.5,40.5) | 5 |
[40.5,43.5] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.
=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.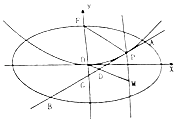
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于A,B两点且与抛物线E在第一象限相切于点P,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M,求 ![]() 的最小值及此时点P的坐标.
的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1:(x﹣2)2+y2=16和圆O2:x2+y2=r2(0<r<2),动圆M与圆O1、圆O2都相切,切圆圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为e1 , e2(e1>e2),则e1+2e2的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() =2csinA
=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ⊥
⊥ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |=t,若P点是△ABC所在平面内一点,且
|=t,若P点是△ABC所在平面内一点,且 ![]() =
= ![]() +
+ ![]() ,当t变化时,
,当t变化时, ![]() 的最大值等于( )
的最大值等于( )
A.﹣2
B.0
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex(a≠0),g(x)=x2(Ⅰ)若曲线c1:y=f(x)与曲线c2:y=g(x)存在公切线,求a最大值.
(Ⅱ)当a=1时,F(x)=f(x)﹣bg(x)﹣cx﹣1,且F(2)=0,若F(x)在(0,2)内有零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为 ![]() ,则p=( )
,则p=( )
A.1
B.![]()
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com