
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .过
.过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

(l)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:四边形![]() 为平行四边形;
为平行四边形;
(Ⅲ)若是![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2) 见解析(3) ![]()
【解析】试题分析:(Ⅰ)由线面垂直的性质 可得![]() ,由菱形的性质可得
,由菱形的性质可得![]() .从而由线面垂直的判定定理可得
.从而由线面垂直的判定定理可得![]() 平面
平面![]() ;(Ⅱ)先证明
;(Ⅱ)先证明![]() 平面
平面![]() ,再根据线面平行的性质可得
,再根据线面平行的性质可得![]() ,根据面面平行的性质可得
,根据面面平行的性质可得![]() ,从而得四边形
,从而得四边形![]() 为平行四边形;(Ⅲ)在平面
为平行四边形;(Ⅲ)在平面![]() 内,过
内,过![]() 作
作![]() .因为
.因为 ![]() 平面
平面![]() ,所以,以
,所以,以![]() 为轴建立空间直角坐标系,可知平面
为轴建立空间直角坐标系,可知平面![]() 的法向量为
的法向量为![]() ,根据向量垂直数量积为零列方程组求出平面
,根据向量垂直数量积为零列方程组求出平面![]() 的法向量,利用空间向量夹角余弦公式可得结果.
的法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(Ⅰ)因为 ![]() 平面
平面![]() ,所以
,所以 ![]() .
.
因为 三棱柱![]() 中,
中, ![]() ,所以 四边形
,所以 四边形![]() 为菱形,
为菱形,
所以 ![]() .
. ![]() 与
与![]() 在平面
在平面![]() 内相交.
内相交.
所以 ![]() 平面
平面![]() .
.
(Ⅱ)因为 ![]() ,
, ![]() 平面
平面![]() ,所以
,所以 ![]() 平面
平面![]() .
.
因为 平面![]() 平面
平面![]() ,所以
,所以 ![]() .
.
因为 平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以 ![]() .
.
所以 四边形![]() 为平行四边形.
为平行四边形.
(Ⅲ)在平面![]() 内,过
内,过![]() 作
作![]() .
.
因为 ![]() 平面
平面![]() ,
,
如图建立空间直角坐标系![]() .
.
由题意得, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
因为 ![]() ,所以
,所以  ,
,
所以 ![]() .
.
由(Ⅰ)得平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 即
即
令![]() ,则
,则![]() ,
, ![]() ,所以
,所以 ![]() .
.
所以  .
.
由图知 二面角![]() 的平面角是锐角,
的平面角是锐角,
所以 二面角![]() 的大小为
的大小为![]() .
.

【方法点晴】本题主要考查线面垂直的判定定理、线面平行的性质、面面平行的直线以及利用空间向量求二面角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】狄利克雷函数是高等数学中的一个典型函数,若![]() ,则称
,则称![]() 为狄利克雷函数.对于狄利克雷函数
为狄利克雷函数.对于狄利克雷函数![]() ,给出下面4个命题:①对任意
,给出下面4个命题:①对任意![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ;③对任意
;③对任意![]() ,都有
,都有![]() ,
, ![]() ;④对任意
;④对任意![]() ,都有
,都有![]() .其中所有真命题的序号是( )
.其中所有真命题的序号是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从
年底某购物网站为了解会员对售后服务(包括退货、换货、维修等)的满意度,从![]() 年下半年的会员中随机调查了
年下半年的会员中随机调查了![]() 个会员,得到会员对售后服务的满意度评分如下:
个会员,得到会员对售后服务的满意度评分如下:
![]()
根据会员满意度评分,将会员的满意度从低到高分为三个等级:
满意度评分 | 低于 |
| 不低于 |
满意度等级 | 不满意 | 比较满意 | 非常满意 |
(1)根据这![]() 个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
个会员的评分,估算该购物网站会员对售后服务比较满意和非常满意的频率;
(2)以(1)中的频率作为概率,假设每个会员的评价结果相互独立.
(i)若从下半年的所有会员中随机选取![]() 个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
个会员,求恰好一个评分比较满意,另一个评分非常满意的概率;
(ii)若从下半年的所有会员中随机选取![]() 个会员,记评分非常满意的会员的个数为
个会员,记评分非常满意的会员的个数为![]() ,求
,求![]() 的分布列,数学期望
的分布列,数学期望![]() 及方差
及方差![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治理大气污染,某市2017年初采用了一系列措施,比如“煤改电”,“煤改气”,“国Ⅰ,Ⅱ轻型汽油车限行”,“整治散乱污染企业”等.下表是该市2016年和2017年12月份的空气质量指数(AQI)(AQI指数越小,空气质量越好)统计表.
表1:2016年12月AQI指数表:单位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 47 | 123 | 232 | 291 | 78 | 103 | 159 | 132 | 37 | 67 | 204 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 270 | 78 | 40 | 51 | 135 | 229 | 270 | 265 | 409 | 429 | 151 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 47 | 155 | 191 | 64 | 54 | 85 | 75 | 249 | 329 |
表2:2017年12月AQI指数表:单位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 91 | 187 | 79 | 28 | 44 | 49 | 27 | 41 | 56 | 43 | 28 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 28 | 49 | 94 | 62 | 40 | 46 | 48 | 55 | 44 | 74 | 62 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 50 | 50 | 46 | 41 | 101 | 140 | 221 | 157 | 55 |
根据表中数据回答下列问题:
(Ⅰ)求出2017年12月的空气质量指数的极差;
(Ⅱ)根据《环境空气质量指数(AQI)技术规定(试行)》规定:当空气质量指数为0~50时,空气质量级别为一级.从2017年12月12日到12月16这五天中,随机抽取三天,空气质量级别为一级的天数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)你认为该市2017年初开始采取的这些大气污染治理措施是否有效?结合数据说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点与抛物线
的右顶点与抛物线![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 且垂直于
且垂直于![]() 轴的直线截抛物线所得的弦长为.
轴的直线截抛物线所得的弦长为.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 恒过一定点.
恒过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校初三年级有![]() 名学生,随机抽查了
名学生,随机抽查了![]() 名学生,测试
名学生,测试![]() 分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
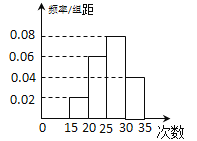
A. 该校初三年级学生![]() 分钟仰卧起坐的次数的中位数为
分钟仰卧起坐的次数的中位数为![]() 次
次
B. 该校初三年级学生![]() 分钟仰卧起坐的次数的众数为
分钟仰卧起坐的次数的众数为![]() 次
次
C. 该校初三年级学生![]() 分钟仰卧起坐的次数超过
分钟仰卧起坐的次数超过![]() 次的人数约有
次的人数约有![]() 人
人
D. 该校初三年级学生![]() 分钟仰卧起坐的次数少于
分钟仰卧起坐的次数少于![]() 次的人数约为
次的人数约为![]() 人.
人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为y=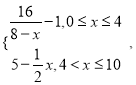 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(1≤a≤4)个单位的药剂,要使接下来的4天中能够持续有效净化,试求a的最小值(精确到0.1,参考数据: ![]() 取1.4).
取1.4).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com