
【题目】给出下列结论:
①“![]() 且
且![]() 为真”是“
为真”是“![]() 或
或![]() 为真”的充分不必要条件:②“
为真”的充分不必要条件:②“![]() 且
且![]() 为假”是“
为假”是“![]() 或
或![]() 为真”的充分不必要条件;③“
为真”的充分不必要条件;③“![]() 或
或![]() 为真”是“非
为真”是“非![]() 为假”的必要不充分条件;④“非
为假”的必要不充分条件;④“非![]() 为真”是“
为真”是“![]() 且
且![]() 为假”的必要不充分条件.
为假”的必要不充分条件.
其中,正确的结论是__________.
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为![]() ,直线MB的斜率为
,直线MB的斜率为![]() ,证明
,证明![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种汽车的元件,该元件是经过![]() 、
、![]() 、
、![]() 三道工序加工而成的,
三道工序加工而成的,![]() 、
、![]() 、
、![]() 三道工序加工的元件合格率分别为
三道工序加工的元件合格率分别为![]() 、
、![]() 、
、![]() .已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工都合格的元件为一等品;恰有两道工序加工合格的元件为二等品;其它的为废品,不进入市场.
(Ⅰ)生产一个元件,求该元件为二等品的概率;
(Ⅱ)若从该工厂生产的这种元件中任意取出3个元件进行检测,求至少有2个元件是一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假:
(1)一次函数![]() (
(![]() 是非零常数)的图象一定经过点
是非零常数)的图象一定经过点![]() ;
;
(2)直角三角形的外心一定在斜边上;
(3)已知![]() ,则
,则![]() 是
是![]() 的充要条件;
的充要条件;
(4)如果![]() 都能被5整除,则
都能被5整除,则![]() 也能被5整除.
也能被5整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, 直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点, 线段
两点, 线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交于
交于![]() 点.
点.
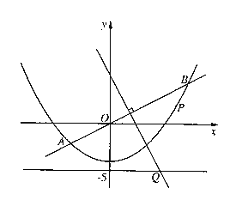
(1)求点![]() 的坐标;
的坐标;
(2)当P为抛物线上位于线段![]() 下方(含
下方(含![]() )的动点时, 求ΔOPQ面积的最大值.
)的动点时, 求ΔOPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.
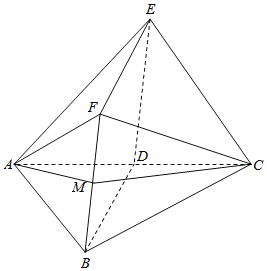
![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
(1)证明:CF⊥平面ADF;
(2)求二面角DAFE的余弦值.
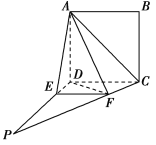
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com