
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人是“微信控”的概率.
【答案】(1)见解析;(2)3,2;(3)![]() .
.
【解析】
(1)列出联表,计算![]() ,所以没有
,所以没有![]() 的把握认为“微信控”与“性别”有关.(2)由图表可知,在
的把握认为“微信控”与“性别”有关.(2)由图表可知,在![]() 名女性用户中,微信控有
名女性用户中,微信控有![]() 人,非微信控有
人,非微信控有![]() 人.(3)利用列举法,列举出
人.(3)利用列举法,列举出![]() 位女性任选
位女性任选![]() 人的基本事件,由此求得抽取
人的基本事件,由此求得抽取![]() 人中恰有
人中恰有![]() 人是“微信控”的概率.
人是“微信控”的概率.
(1)由列联表可得:
![]() 所以没有
所以没有![]() 的把握认为“微信控”与“性别”有关.
的把握认为“微信控”与“性别”有关.
(2)根据题意所抽取的![]() 位女性中,“微信控”有
位女性中,“微信控”有![]() 人,“非微信控”有
人,“非微信控”有![]() 人.
人.
(3)抽取的![]() 位女性中,“微信控”
位女性中,“微信控”![]() 人分别记为
人分别记为![]() ,
,![]() ,
,![]() ;“非微信控”
;“非微信控”![]() 人分别记为
人分别记为![]() ,
,![]() .
.
则再从中随机抽取![]() 人构成的所有基本事件为:
人构成的所有基本事件为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有
,共有![]() 种;
种;
抽取![]() 人中恰有
人中恰有![]() 人为“微信控”所含基本事件为:
人为“微信控”所含基本事件为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有
,共有![]() 种,所求为
种,所求为![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,点
,点![]() .已知抛物线
.已知抛物线![]() (
(![]() 是常数),顶点为
是常数),顶点为![]() .
.
(1)当抛物线经过点![]() 时,求顶点
时,求顶点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴下方,当
轴下方,当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(3)无论![]() 取何值,该抛物线都经过定点
取何值,该抛物线都经过定点![]() .当
.当![]() 时,求抛物线的解析式.
时,求抛物线的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王久良导演的纪录片《垃圾围城》真实地反映了城市垃圾污染问题,目前中国668个城市中有超过![]() 的城市处于垃圾的包围之中,且城市垃圾中的快递行业产生的包装垃圾正在逐年攀升,有关数据显示,某城市从2016年到2019年产生的包装垃圾量如下表:
的城市处于垃圾的包围之中,且城市垃圾中的快递行业产生的包装垃圾正在逐年攀升,有关数据显示,某城市从2016年到2019年产生的包装垃圾量如下表:
年份x | 2016 | 2017 | 2018 | 2019 |
包装垃圾y(万吨) | 4 | 6 | 9 | 13.5 |
(1)有下列函数模型:①![]() ;②
;②![]() ;③
;③![]() .
.![]() 试从以上函数模型中,选择模型________(填模型序号),近似反映该城市近几年包装垃圾生产量y(万吨)与年份x的函数关系,并直接写出所选函数模型解析式;
试从以上函数模型中,选择模型________(填模型序号),近似反映该城市近几年包装垃圾生产量y(万吨)与年份x的函数关系,并直接写出所选函数模型解析式;
(2)若不加以控制,任由包装垃圾如此增长下去,从哪年开始,该城市的包装垃圾将超过40万吨?(参考数据:![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
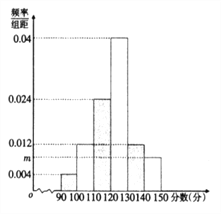
(1)求![]() 的值及这50名同学数学成绩的平均数
的值及这50名同学数学成绩的平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,若已知成在
的同学中选出3位作为代表进行座谈,若已知成在![]() 的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,a1=3,且Sn=nan+1-n2-n.
(1)求{an}的通项公式;
(2)若数列{bn}满足![]() ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间D上的函数![]() ,若存在正整数k,使不等式
,若存在正整数k,使不等式![]() 恒成立,则称
恒成立,则称![]() 为
为![]() 型函数.
型函数.
(1)设函数![]() ,定义域
,定义域![]() .若
.若![]() 是
是![]() 型函数,求实数a的取值范围;
型函数,求实数a的取值范围;
(2)设函数![]() ,定义域
,定义域![]() .判断
.判断![]() 是否为
是否为![]() 型函数,并给出证明.
型函数,并给出证明.
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形,若图中直角三角形两锐角分别为![]() ,
,![]() ,且小正方形与大正方形面积之比为
,且小正方形与大正方形面积之比为![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com