
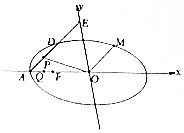
 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1��a��2$\sqrt{3}$������ΪF����ΪA��$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$������OΪԭ�㣬eΪ��Բ�������ʣ�����A��б��Ϊk��k��0����ֱ��l����ԲC�ڵ�D����y���ڵ�E��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1��a��2$\sqrt{3}$������ΪF����ΪA��$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$������OΪԭ�㣬eΪ��Բ�������ʣ�����A��б��Ϊk��k��0����ֱ��l����ԲC�ڵ�D����y���ڵ�E������ ��1����$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$���ɵã�$\frac{1}{c}+\frac{1}{a}$=$\frac{3c}{a��a-c��}$���ɵã�a=2c����a2=12+c2��������ɵó���
��2�����ڶ�ֵ��=$\frac{1}{2}$ʹ��OP��EQ��������������������ֱ��AD�ķ���Ϊ��y=k��x+4������E��0��4k����ֱ�߷�������Բ����������Ϊ����3+4k2��x2+32k2x+64k2-48=0�����ø���ϵ���Ĺ�ϵ�ɵã�D��$\frac{12-16{k}^{2}}{3+4{k}^{2}}$��$\frac{24k}{3+4{k}^{2}}$��������$\overrightarrow{AP}$=��$\overrightarrow{AD}$���ɵ�$\overrightarrow{OP}$=$\overrightarrow{OA}$+$��\overrightarrow{AD}$.$\overrightarrow{EQ}$=��-3��-4k��������$\overrightarrow{EQ}$��$\overrightarrow{OP}$����$\overrightarrow{EQ}$•$\overrightarrow{OP}$=0�����ɵó���
��� �⣺��1����$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$���ɵã�$\frac{1}{c}+\frac{1}{a}$=$\frac{3c}{a��a-c��}$���ɵã�a=2c����a2=12+c2�����a2=16��c=2��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1��
��2�����ڶ�ֵ��=$\frac{1}{2}$ʹ��OP��EQ��������������֤����
ֱ��AD�ķ���Ϊ��y=k��x+4������E��0��4k����
����$\left\{\begin{array}{l}{y=k��x+4��}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$��������3+4k2��x2+32k2x+64k2-48=0��
��-4xD=$\frac{64{k}^{2}-48}{3+4{k}^{2}}$�����xD=$\frac{12-16{k}^{2}}{3+4{k}^{2}}$����yD=$\frac{24k}{3+4{k}^{2}}$����D��$\frac{12-16{k}^{2}}{3+4{k}^{2}}$��$\frac{24k}{3+4{k}^{2}}$����
��$\overrightarrow{AP}$=��$\overrightarrow{AD}$���ɵ�$\overrightarrow{OP}$=$\overrightarrow{OA}$+$��\overrightarrow{AD}$=$��\frac{24��-12-16{k}^{2}}{3+4{k}^{2}}��\frac{24��k}{3+4{k}^{2}}��$��
$\overrightarrow{EQ}$=��-3��-4k����
����$\overrightarrow{EQ}$��$\overrightarrow{OP}$����$\overrightarrow{EQ}$•$\overrightarrow{OP}$=$\frac{-3��24��-12-16{k}^{2}��}{3+4{k}^{2}}$-$\frac{96��{k}^{2}}{3+4{k}^{2}}$=0��
��Ϊ����6+8k2����=3+4k2����æ�=$\frac{1}{2}$��
��˴��ڶ�ֵ��=$\frac{1}{2}$ʹ��OP��EQ�������
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⡢һԪ���η��̵ĸ���ϵ���Ĺ�ϵ�������������ʡ�������ֱ���������Ĺ�ϵ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
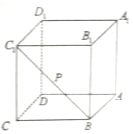 ��ͼ����P��������ABCD-A1B1C1D1����Խ���BC1���߶�BC1�����˶�����������������⣺
��ͼ����P��������ABCD-A1B1C1D1����Խ���BC1���߶�BC1�����˶�����������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
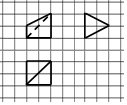 ��ͼ������ֽ��С�����εı߳�Ϊ1����ʵ��������������ij�����������ͼ����ö����������ı����Ϊ��������
��ͼ������ֽ��С�����εı߳�Ϊ1����ʵ��������������ij�����������ͼ����ö����������ı����Ϊ��������| A�� | 8�� | B�� | $\frac{25}{2}$�� | C�� | 12�� | D�� | $\frac{41}{4}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com