
分析 由绝对值的含义,去绝对值,再由二次函数的最值求法,对a讨论,结合单调性,即可得到最值.
解答 解:y=(x-2)|x|=$\left\{\begin{array}{l}{{x}^{2}-2x,x>0}\\{2x-{x}^{2},x≤0}\end{array}\right.$,
当x≤0,y=-(x-1)2+1,
当x>0,y=(x-1)2-1,
当1≤a≤2时,函数在[a,2]递增,ymin=a2-2a,ymax=0;
当1-$\sqrt{2}$≤a<1时,在[a,0)递增,(0,1)递减,(1,2)递增,
即有ymin=1-2=-1,ymax=0;
当a<1-$\sqrt{2}$时,在[a,0)递增,(0,1)递减,(1,2)递增,
即有ymin=(a-2)|a|=2a-a2,ymax=0.
点评 本题考查含绝对值函数的最值的求法,注意分类讨论的思想方法,以及函数的单调性的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 96 | B. | 108 | C. | 145 | D. | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
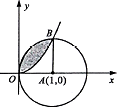 如图所示,阴影部分是由曲线y=x2(x>0)与圆(x-1)2+y2=1构成的区域,在圆中任取一点M,则M点落在阴影部分区域的概率为$\frac{1}{4}$-$\frac{1}{3π}$.
如图所示,阴影部分是由曲线y=x2(x>0)与圆(x-1)2+y2=1构成的区域,在圆中任取一点M,则M点落在阴影部分区域的概率为$\frac{1}{4}$-$\frac{1}{3π}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | 15 | 15 | 30 |
| 非优秀 | |||
| 总计 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm),若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118)内该厂可获利分别为10,30,20,10(单位:元),现在该厂生产的产品中随机抽取200件测量它们的直径,得到如图所示的频率直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm),若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118)内该厂可获利分别为10,30,20,10(单位:元),现在该厂生产的产品中随机抽取200件测量它们的直径,得到如图所示的频率直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com