【题目】如图，
中，
，
，若以
，
为焦点的双曲线的渐近线经过点
，则该双曲线的离心率为
A. 
B. 
C. 
D. 
【答案】D
【解析】
设AB=BC=2，取AB的中点为O，由题意可得双曲线的一条渐近线为直线OC，由余弦定理可得OC，cos∠COB，求得tan∠COB，即为渐近线的斜率，由a，b，c的关系和离心率公式，即可得到．
设AB=BC=2，
取AB的中点为O，
由题意可得双曲线的一条渐近线为直线OC，
在三角形OBC中，
cosB=﹣
，
∴OC2=OB2+BC2﹣2OBBCcosB=1+4﹣2×1×2×（﹣）=7，
∴OC=
，
则cos∠COB=
=
，
可得sin∠COB=
=
，
tan∠COB=
=
，
可得双曲线的渐近线的斜率为，
不妨设双曲线的方程为
﹣
=1（a，b＞0），
渐近线方程为y=±
x，
可得=，
可得e=
=
=
=
=
．
故选：D．
智能训练练测考系列答案科目：高中数学 来源： 题型：
【题目】重庆朝天门批发市场某服装店试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于成本的40%.经试销发现，销售量y（件）与销售单价x（元）符合一次函数
，且
时，
；
时，
.
（1）求一次函数的表达式；
（2）若该服装店获得利润为W元，试写出利润与销售单价x之间的关系式；销售单价定为多少元时，服装店可获得最大利润，最大利润是多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点A,B,C,D是直角坐标系中不同的四点，若
，
，且
，则下列说法正确的是( ),
A.C可能是线段AB的中点
B.D可能是线段AB的中点
C.C、D可能同时在线段AB上
D.C、D不可能同时在线段AB的延长线上
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学的高二（1）班男同学有45名，女同学有15名，老师按照分层抽样的方法组建了一个4人的课外兴趣小组.
（1）求课外兴趣小组中男、女同学的人数；
（2）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出1名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
（3）试验结束后，第一次做试验的同学得到的试验数据为68，70，71，72，74，第二次做试验的同学得到的试验数据为69,70,70,72,74 ，请问哪位同学的实验更稳定？并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一个口袋有
个白球，
个黑球，这些球除颜色外全部相同，现将口袋中的球随机逐个取出，并依次放入编号为，
，，
的抽屉内.
（1）求编号为的抽屉内放黑球的概率；
（2）口袋中的球放入抽屉后，随机取出两个抽屉中的球，求取出的两个球是一黑一白的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，三棱柱
的各棱长均为2，侧面
底面
，侧棱
与底面所成的角为
．
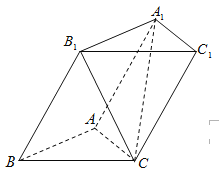
（Ⅰ）求直线
与底面所成的角；
（Ⅱ）在线段
上是否存在点
，使得平面
平面
？若存在，求出
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设命题
对任意实数
，不等式
恒成立；命题
方程
表示焦点在
轴上的双曲线．
（1）若命题
为真命题，求实数
的取值范围；
（2）若命题：“
”为真命题，且“
”为假命题，求实数
的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
