
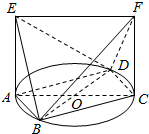
 如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.
如图,已知AC,BD为圆O的任意两条直径,直线AE,CF是圆O所在平面的两条垂线,且线段AE=CF=$\sqrt{2}$,AC=2.分析 (Ⅰ)证明AD⊥平面ABE,即可证明AD⊥BE;
(Ⅱ)多面体EF-ABCD体积V=VB-AEFC+VD-AEFC=2VB-AEFC,作BM⊥AC交AC于点M,则BM⊥平面AEFC,求出多面体ABCDEF的体积,即可得出结论.
解答 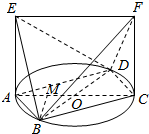 (Ⅰ)证明:∵BD为圆O的直径,∴AB⊥AD,
(Ⅰ)证明:∵BD为圆O的直径,∴AB⊥AD,
∵直线AE是圆O所在平面的垂线,
∴AD⊥AE,
∵AB∩AE=A,
∴AD⊥平面ABE,
∴AD⊥BE;
(Ⅱ)解:多面体EF-ABCD体积V=VB-AEFC+VD-AEFC=2VB-AEFC.
∵直线AE,CF是圆O所在平面的两条垂线,
∴AE∥CF,∥AE⊥AC,AF⊥AC.
∵AE=CF=$\sqrt{2}$,∴AEFC为矩形,
∵AC=2,
∴SAEFC=2$\sqrt{2}$,
作BM⊥AC交AC于点M,则BM⊥平面AEFC,
∴V=2VB-AEFC=2×$\frac{1}{3}×2\sqrt{2}×BM$≤$\frac{4\sqrt{2}}{3}OB$=$\frac{4\sqrt{2}}{3}$.
∴多面体EF-ABCD体积的最大值为$\frac{4\sqrt{2}}{3}$.
点评 本题考查线面垂直,线线垂直,考查体积的计算,考查学生分析解决问题的能力,难度中等.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{15}$ | C. | $3\sqrt{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.
如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
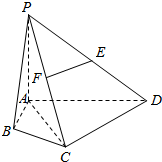 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,$\frac{\sqrt{6}}{2}$] | C. | [$\frac{\sqrt{6}}{2}$,+∞) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
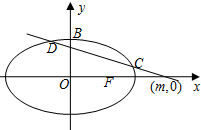 如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.
如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com