Question

【题目】已知数列{an}前n项和为Sn=﹣n2+12n．
（1）求{an}的通项公式；
（2）求数列{|an|}的前10项和T10 ．

Answer 1

【答案】
（1）解：当n=1时，a1=S1=12×1﹣12=11；当n≥2时，an=Sn﹣Sn﹣1=（12n﹣n2）﹣[12（n﹣1）﹣（n﹣1）2]=13﹣2n．

经验证当n=1时，a1=11也符合13﹣2n的形式

（2）解：数列{an}的通项公式为an=13﹣2n，

∵当n≤6时，an＞0，当n≥7时，an＜0，

∴T10=a1+…+a6﹣a7﹣a8﹣a9﹣a10=2S6﹣S10=52

【解析】（1）求出a1 ， 利用n≥2时，an=Sn﹣Sn﹣1 ， 求出an ， 验证n=1时满足通项公式，即可求得数列{an}的通项公式（2）由（1）判断哪些项为正，哪些项为负，然后求解Tn ．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系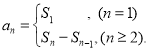)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．