
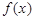 满足在集合
满足在集合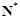 上的值域仍是集合
上的值域仍是集合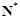 ,则把函数
,则把函数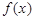 称为N函数.
称为N函数.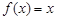 就是N函数.
就是N函数.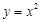 ,②
,②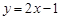 ,③
,③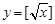 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);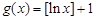 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;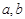 ,函数
,函数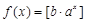 都不是N函数.
都不是N函数.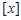 ”表示不超过
”表示不超过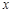 的最大整数)
的最大整数)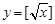 ;(Ⅱ)是N函数;(Ⅲ)略
;(Ⅱ)是N函数;(Ⅲ)略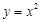 的定义域为
的定义域为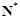 时,值域不是集合
时,值域不是集合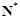 ,例如值域中不含2。故
,例如值域中不含2。故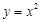 不是N函数 。
不是N函数 。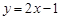 的定义域为
的定义域为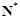 时,值域不是集合
时,值域不是集合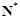 ,例如值域中不含2。故
,例如值域中不含2。故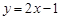 不是N函数。当
不是N函数。当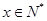 时
时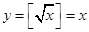 ,所以
,所以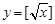 是N函数。(Ⅱ)因为“
是N函数。(Ⅱ)因为“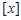 ”表示不超过
”表示不超过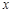 的最大整数,所以
的最大整数,所以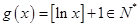 。设
。设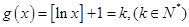 ,则
,则 ,所以
,所以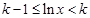 ,解得
,解得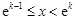 ,因为
,因为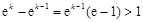 所以在
所以在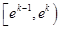 一定存在正整数
一定存在正整数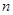 ,即存在
,即存在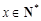 满足
满足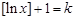 (Ⅲ)需对实数
(Ⅲ)需对实数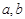 在全体实数范围内进行讨论。若
在全体实数范围内进行讨论。若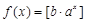 为负时,函数
为负时,函数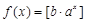 不是N函数;若函数
不是N函数;若函数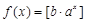 有最大值时,函数
有最大值时,函数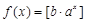 不是N函数;若函数
不是N函数;若函数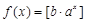 的值是正数但不能取到所有正数时,函数
的值是正数但不能取到所有正数时,函数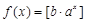 不是N函数。
不是N函数。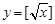 是N函数. 3分
是N函数. 3分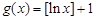 是N函数.
是N函数.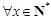 ,
,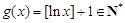 . 4分
. 4分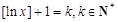 ,
,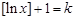 可得
可得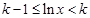 ,
,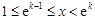 .
.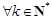 ,恒有
,恒有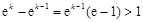 成立,
成立,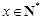 ,满足
,满足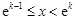 ,
,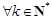 ,总存在
,总存在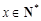 满足
满足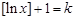 ,
,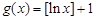 是N函数. 8分
是N函数. 8分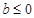 时,有
时,有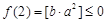 ,
, 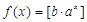 都不是N函数. 9分
都不是N函数. 9分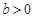 时,① 若
时,① 若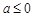 ,有
,有 ,
,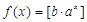 都不是N函数. 10分
都不是N函数. 10分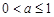 ,由指数函数性质易得
,由指数函数性质易得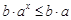 ,
, ,都有
,都有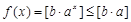
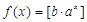 都不是N函数. 11分
都不是N函数. 11分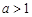 ,令
,令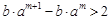 ,则
,则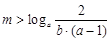 ,
,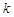 使得
使得 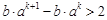 ,
,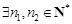 ,使得
,使得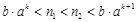 ,
,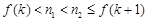 .
.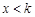 时,
时,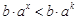 ,所以
,所以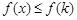 ;
;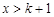 时,
时,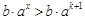 ,所以
,所以 ,
, ,都有
,都有 ,
,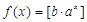 都不是N函数. 13分
都不是N函数. 13分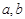 ,函数
,函数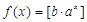 都不是N函数.
都不是N函数.

科目:高中数学 来源:不详 题型:解答题
 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1. 的单调区间,
的单调区间, ≥k在区间
≥k在区间 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 吨,此时所需生产费用为(
吨,此时所需生产费用为( )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为 万元,这里
万元,这里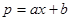 (
( 为常数,
为常数, )
) 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 从点
从点 出发,分别按逆时针方向沿周长均为
出发,分别按逆时针方向沿周长均为 的正三角形、正方形运动一周,
的正三角形、正方形运动一周, 两点连线的距离
两点连线的距离 与点
与点 走过的路程
走过的路程 的函数关系分别记为
的函数关系分别记为 ,定义函数
,定义函数 对于函数
对于函数 ,下列结论正确的个数是( )
,下列结论正确的个数是( )
 ;
; 的图像关于直线
的图像关于直线 对称;
对称; 值域为
值域为 ;
; 在区间
在区间 上单调递增.
上单调递增.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com