
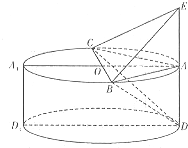
 如图,一个几何体由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在⊙O的圆周上,E,A,D三点共线,已知AB⊥AC,AB=AC,AE=AD=1,BC=2.
如图,一个几何体由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在⊙O的圆周上,E,A,D三点共线,已知AB⊥AC,AB=AC,AE=AD=1,BC=2.| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |


科目:高中数学 来源: 题型:
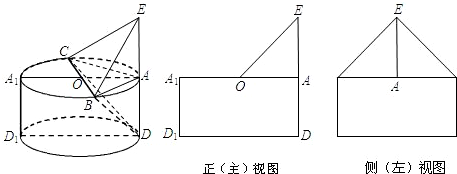
 已知一个几何体是由上下两部分构成的组合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为
已知一个几何体是由上下两部分构成的组合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为| 5 |
A、
| ||
B、
| ||
| C、2π | ||
| D、4π |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
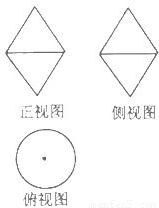
 (2013•泰安二模)如图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为( )
(2013•泰安二模)如图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为( )查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2013年山东省泰安市高考数学二模试卷(文科)(解析版) 题型:选择题


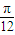
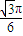
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com