
【题目】记方程①x2+a1x+1=0,②x2+a2x+1=0,③x2+a3x+1=0,其中a1,a2,a3是正实数,当a1,a2,a3成等比数列,下列选项中,当方程③有实根时,能推出的是( )
A.方程①有实根或方程②无实根B.方程①有实根或方程②有实根
C.方程①无实根或方程②无实根D.方程①无实根或方程②有实根
【答案】C
【解析】
试题当方程③有实根时,![]() ≥0,又a3>0,解得a3≥2.由于a1,a2,a3成等比数列,可得
≥0,又a3>0,解得a3≥2.由于a1,a2,a3成等比数列,可得![]() .对于方程①x2+a1x+1=0,△1=
.对于方程①x2+a1x+1=0,△1=![]() ;对于方程②x2+a2x+1=0,△2=
;对于方程②x2+a2x+1=0,△2=![]() ﹣4.对△2分类讨论即可得出.
﹣4.对△2分类讨论即可得出.
解:当方程③有实根时,![]() ≥0,又a3>0,解得a3≥2.
≥0,又a3>0,解得a3≥2.
∵a1,a2,a3成等比数列,∴![]() .
.
对于方程①x2+a1x+1=0,△1=![]() ;对于方程②x2+a2x+1=0,△2=
;对于方程②x2+a2x+1=0,△2=![]() ﹣4.
﹣4.
假设△2<0,则0<a2<2,则a1=![]() <2,可得△1<0,因此方程①无实数根;
<2,可得△1<0,因此方程①无实数根;
假设△2≥0,则a2≥2,则a1=![]() 与2的大小不确定,因此△1与0大小关系不确定,即方程①可能有实数根也可能无实数根.
与2的大小不确定,因此△1与0大小关系不确定,即方程①可能有实数根也可能无实数根.
故选C.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 的正半轴建立平面直角坐标系
的正半轴建立平面直角坐标系![]() .
.
(1)求![]() 和
和![]() 的参数方程;
的参数方程;
(2)已知射线![]() ,将
,将![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,且
,且![]() 与
与![]() 交于
交于![]() 两点,
两点, ![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 取得最大值时点
取得最大值时点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若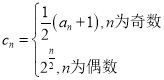
![]() ,从数列
,从数列![]() 中抽出部分项(奇数项与偶数项均不少于两项),将抽出的项按照某一顺序排列后构成等差数列.当等差数列的项数最大时,求所有满足条件的等差数列.
中抽出部分项(奇数项与偶数项均不少于两项),将抽出的项按照某一顺序排列后构成等差数列.当等差数列的项数最大时,求所有满足条件的等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为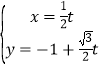 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,以直角坐标系的原点为极点,以
两点,以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2) 已知点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系xOy中,曲线C的参数方程为![]() (a为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
(a为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(1)求C的普通方程和l的倾斜角;
(2)设点![]() ,l和C交于A,B两点,求
,l和C交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
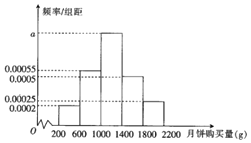
【题目】2018年中秋节到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量![]() 单位:
单位:![]() 进行了问卷调查,得到如下频率分布直方图:
进行了问卷调查,得到如下频率分布直方图:
![]() 求频率分布直方图中a的值;
求频率分布直方图中a的值;
![]() 以频率作为概率,试求消费者月饼购买量在
以频率作为概率,试求消费者月饼购买量在![]() 的概率;
的概率;
![]() 已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的
已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的![]() ,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求
,请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求![]() 频率分布直方图中同一组的数据用该组区间的中点值作代表
频率分布直方图中同一组的数据用该组区间的中点值作代表![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com