数列{an}的前n项和为sn,a1=1,an+1=2sn+1,(n≥1),等差数列{bn}的各项均为正数,前n项和为Bn,且B3=15,又a1+b1,a2+b2,a3+b3成等比数列.
(1)求数列{an}与{bn}的通项公式;
(2)若Tn=a1b1+a2b2+a3b3+…+anbn,求Tn的表达式.
解:(Ⅰ)∵a
1=1,a
n+1=2S
n+1(n∈N
*),
∴a
n=2S
n-1+1(n∈N
*,n>1),
∴a
n+1-a
n=2(S
n-S
n-1),
∴a
n+1-a
n=2a
n,
∴a
n+1=3a
n(n∈N
*,n>1)(2分)
而a
2=2a
1+1=3=3a
1,
∴a
n+1=3a
n(n∈N
*)
∴数列{a
n}是以1为首项,3为公比的等比数列,
∴a
n=3
n-1(n∈N
*)(4分)
∴a
1=1,a
2=3,a
3=9,
在等差数列{b
n}中,
∵b
1+b
2+b
3=15,
∴b
2=5.
又因a
1+b
1、a
2+b
2、a
3+b
3成等比数列,设等差数列{b
n}的公差为d,
∴(1+5-d)(9+5+d)=64(6分)
解得d=-10,或d=2,
∵b
n>0(n∈N*),
∴舍去d=-10,取d=2,
∴b
1=3,
∴b
n=2n+1(n∈N
*).(8分)
(Ⅱ)∵T
n=a
1b
1+a
2b
2+a
3b
3+…+a
nb
n,
∴由(Ⅰ)知T
n=3×1+5×3+7×3
2++(2n-1)3
n-2+(2n+1)3
n-1,①
3T
n=3×3+5×3
2+7×3
3++(2n-1)3
n-1+(2n+1)3
n,②(10分)
①-②得-2T
n=3×1+2×3+2×3
2+2×3
3++2×3
n-1-(2n+1)3
n,(12分)
=3+2(3+3
2+3
3++3
n-1)-(2n+1)3
n
=3+2×
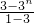
-(2n+1)3n=3n-(2n+1)3n=-2n•3n,
∴T
n=n•3
n.(14分)
分析:(1)求解时要利用恒等式a
n+1=2S
n+1构造出a
n=2S
n-1+1两者作差得出a
n+1=3a
n,此处是难点,数列的{b
n}的求解根据题意列出方程求d即可.
(II)数列求和是一个典型的错位相减法求和技巧的运用,借助错位相减法能求出结果.
点评:本题考查数列知识的综合运用,技巧性较强,是数列中的一道难度较高的题,对答题者基础知识与基本技能要求较高,是用来提高学生数列素养的一道好题.

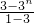 -(2n+1)3n=3n-(2n+1)3n=-2n•3n,
-(2n+1)3n=3n-(2n+1)3n=-2n•3n,
