
【题目】已知圆![]() 经过点
经过点![]() ,
,![]() ,且它的圆心在直线
,且它的圆心在直线![]() 上.
上.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)求圆![]() 关于直线
关于直线![]() 对称的圆的方程.
对称的圆的方程.
(Ⅲ)若点![]() 为圆
为圆![]() 上任意一点,且点
上任意一点,且点![]() ,求线段
,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
试题(Ⅰ)首先设出方程,将点坐标代入得到关于参数的方程组,通过解方程组得到参数值,从而确定其方程;(Ⅱ)求出N(2,4)关于x-y+3=0的对称点为(1,5),即可得到圆N关于直线x-y+3=0对称的圆的方程;(Ⅲ)首先设出点M的坐标,利用中点得到点D坐标,代入圆的方程整理化简得到的中点M的轨迹方程
试题解析::(Ⅰ)由已知可设圆心N(a,3a-2),又由已知得|NA|=|NB|,
从而有![]() ,解得:a=2.
,解得:a=2.
于是圆N的圆心N(2,4),半径![]() .
.
所以,圆N的方程为![]() .(5分)
.(5分)
(Ⅱ)N(2,4)关于x-y+3=0的对称点为(1,5),
所以圆N关于直线x-y+3=0对称的圆的方程为![]() (9分)
(9分)
(Ⅲ)设M(x,y),D![]() ,则由C(3,0)及M为线段CD的中点得:
,则由C(3,0)及M为线段CD的中点得: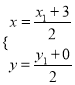 ,解得
,解得![]() 又点D在圆N:
又点D在圆N:![]() 上,所以有
上,所以有![]() ,
,
化简得:![]() .
.
故所求的轨迹方程为![]() .(13分)
.(13分)


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)设角![]() 的顶点在坐标原点,始边在
的顶点在坐标原点,始边在![]() 轴的正半轴上,终边过点
轴的正半轴上,终边过点 ,求
,求![]() 的值;
的值;
(2)试讨论函数![]() 的基本性质(单调性、周期性)(直接写出结论).
的基本性质(单调性、周期性)(直接写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程![]() .
.
![]() 若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
若a是从0,1,2三个数中任取的一个数,b是从0,1,2,3四个数中任取的一个数,求上述方程有实根的概率;
![]() 若a是从区间
若a是从区间![]() 任取的一个数,b是从区间
任取的一个数,b是从区间![]() 任取的一个数,求上述方程有实数的概率.
任取的一个数,求上述方程有实数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加数学竞赛培训,现得到他们在培训期间参加的8次比赛成绩如下:甲:81,79,95,88,84,93,78,82;乙:80,83,92,85,75,95,80,90.
(1)试画出甲、乙两位同学比赛成绩的茎叶图,你能从茎叶图中获取哪些信息?(不少于三条)
(2)在甲同学的8次比赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有可能的结果,并求抽出的2个成绩均大于85分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(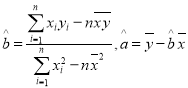 )
)
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com