练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，直线经过点，其倾斜角为．以原点为极点，以轴非负半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系．设曲线的极坐标方程为．

    （1）写出直线的参数方程，若直线与曲线有公共点，求的取值范围．

    （2）设为曲线上任意一点，求的取值范围．

    【答案】（1）（为参数），．（2）

    【解析】

    （1）根据直线的参数方程公式直接得到参数方程，利用极坐标方程化简得到，带入化简得到，解得答案.

    （2）根据参数方程（为参数），得到，得到答案.

    （1）因为曲线的极坐标方程为，

    所以曲线的直角坐标方程为．

    因为直线经过点，其倾斜角为，所以直线的参数方程为

    （为参数），代入，整理得，

    因为直线与曲线有公共点，所以，

    即或，

    因为，所以的取值范围是．

    （2）是曲线上一点，则（为参数），

    所以，

    所以的取值范围是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】淘汰落后产能，对生产设备进行升级改造是企业生存发展的重要前提.某企业今年对旧生产设备的一半进行了升级，剩下的一半在今后的两年内完成升级.为了分析新旧设备的生产质量，从新旧设备生产的产品中各抽取了件作为样本，对最重要的一项质量指标进行检测，该项质量指标值落在内的产品为合格品，否则为不合格品.检测数据如下：

    表1：日设备生产的产品样本频数分布表

    质量指标

    频数

    3

    16

    44

    12

    22

    3

    表2：新设备生产的产品样本频数分布表

    质量指标

    频数

    1

    20

    52

    16

    10

    1

    （1）根据表1和表2提供的数据，试从产品合格率的角度对新旧设备的优劣进行比较；

    （2）面向市场销售时，只有合格品才能销售，这时需要对合格品的品质进行等级细分，质量指标落在内的定为优质品，质量指标落在或内的定为一等品，其它的合格品定为二等品.完成下面的列联表，并判断是否有的把握认为该企业生产的这种产品的质量指标值与新旧设备有关；

    旧设备

    新设备

    合计

    优质品及一等品

    二等品及不合格品

    合计

    /span>

    （3）优质品每件售价元，一等品每件售价元，二等品每件售价元根据表1和表2中的数据，用该组样本中优质品、一等品、二等品各自在合格品中的频率代替从合格产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品，设其支付的费用为（单位：元），求的分布列和数学期望（结果保留整数）.

    附：

    0.150

    0.100

    0.050

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

    ，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）讨论函数的单调性；

    （2）是否存在实数，使得“对任意恒成立”？若存在，求出的取值范围；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过点P(-4,0)的动直线l与抛物线相交于D、E两点，已知当l的斜率为时，.

    （1）求抛物线C的方程；

    （2）设的中垂线在轴上的截距为,求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知拋物线：（），过点且斜率为1的直线与拋物线交于，两点，且为的中点.

    （1）求拋物线的方程；

    （2）设直线与轴交点为，若过的直线与拋物线交于，两点，求证：为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法：

    ①将一组数据中的每一个数据都加上或减去同一个常数后，方差不变；

    ②设有一个线性回归方程，变量x增加1个单位时，y平均增加5个单位；

    ③设具有相关关系的两个变量x，y的相关系数为r，则|r|越接近于0，x和y之间的线性相关程度越强；

    ④在一个2×2列联表中，由计算得K2的值，则K2的值越大，判断两个变量间有关联的把握就越大．

    以上错误结论的个数为(　　)

    A. 0 B. 1 C. 2 D. 3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若，且，求证：；

    （2）若时，恒有，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题：

    ①对立事件一定是互斥事件；②若A，B为两个随机事件，则P(A∪B)＝P(A)＋P(B)；③若事件A，B，C彼此互斥，则P(A)＋P(B)＋P(C)＝1；④若事件A，B满足P(A)＋P(B)＝1，则A与B是对立事件．

    其中正确命题的个数是(　　)

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线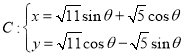（为参数），以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，直线的极坐标方程为：.

    （1）求直线和曲线的直角坐标方程；

    （2），直线和曲线交于、两点，求的值.

    查看答案和解析>>

    同步练习册答案