
【题目】已知曲线![]() 的方程为:
的方程为:![]() (
(![]() ,
,![]() 为常数).
为常数).
(Ⅰ)判断曲线![]() 的形状;
的形状;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求曲线
,求曲线![]() 的方程.
的方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某城市有一直角梯形绿地![]() ,其中
,其中![]() ,
,![]() km,
km,![]() km.现过边界
km.现过边界![]() 上的点
上的点![]() 处铺设一条直的灌溉水管
处铺设一条直的灌溉水管![]() ,将绿地分成面积相等的两部分.
,将绿地分成面积相等的两部分.
(1)如图①,若![]() 为
为![]() 的中点,
的中点,![]() 在边界
在边界![]() 上,求灌溉水管
上,求灌溉水管![]() 的长度;
的长度;
(2)如图②,若![]() 在边界
在边界![]() 上,求灌溉水管
上,求灌溉水管![]() 的最短长度.
的最短长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用![]() 表示.
表示.
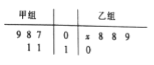
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中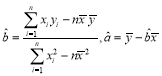 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图. 为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求a>b的概率;
(3)若a=1,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断b为何值时,
,根据茎叶图推断b为何值时,![]() 达到最值.
达到最值.
(只需写出结论)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com