Question

在平行四边形ABCD中，点E在边AB上，且AE：EB=1：2，DE与AC交于点F，若△AEF的面积为6cm²，则△ABC的面积为    cm²．

Answer 1

【答案】分析：由三角形AEF和三角形FCD相似，可得AF：FC=AE：CD=1：3，△BEF的面积等于△AEF的面积的2倍，△FBC的面积等于△AFB的面积的3倍．∴△ABC的面积为△AFB的面积加上△FBC的面积．
解答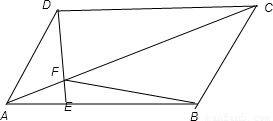：解：如图：连接BF，∵点E在边AB上，且AE：EB=1：2，
由三角形AEF和三角形FCD相似，可得AF：FC=AE：CD=1：3，
∵△FAE 的面积为6cm² ，
∴△FBE 的面积等于12cm² ，
△AFB的面积为6+12=18cm² ，
又△BFC的面积等于△AFB的面积的3倍，
∴△FBC的面积为3×18=54cm² ，
∴△ABC的面积等于△BAF 的面积18cm² 加上△BFC的面积54cm² ，等于 72cm² ．
故答案为 72 cm² ．
点评：本题考查三角形相似的性质，线段的定比分点，以及三角形面积的求法．