
����Ŀ���Ը�ɫ��ѧ��ʼ���ּ��ǽ��յ���̨�����Ŀ���dz����š�����Լ�α������ĵ����ӽǶ��أ�����Ϭ������������������̵�ӡ��ij����Ϊ���˽���ڶ��ּε�ϲ���̶ȣ���������˹ۿ��˸ý�Ŀ��140�����ڣ��õ����µ�������������λ������
�� | Ů | �ܼ� | |
ϲ�� | 40 | 60 | 100 |
��ϲ�� | 20 | 20 | 40 |
�ܼ� | 60 | 80 | 140 |
������60���й����а����ּ��Ƿ�ϲ����ȡ�ֲ��������ȡһ������Ϊ6����������������ϲ���벻ϲ���Ĺ��ڸ��ж�������
���������������������ܷ��ڷ�����ĸ��ʲ�����0.025%��ǰ������Ϊ�����Ա���ϲ���ּ��йأ�����ȷ��0.001��
���ӣ����е�6�����Թ��������ѡȡ���������ٵ��飬��ѡ�����������ڶ�ϲ���ּεĸ��ʣ�
����
p��k2��k0�� | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
k2= ![]() ��
��
���𰸡��⣺��������Ϊ ![]() =
= ![]() ��
��
��������ϲ���Ĺ۴���40�� ![]() =4������ϲ���Ĺ�����6��4=2����
=4������ϲ���Ĺ�����6��4=2����
�����裺�����Ա���ϲ���ּ��أ�����֪���ݿ���ã�
k2= ![]() =
= ![]() ��1.167��5.024��
��1.167��5.024��
����ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ�����Ա���ϲ���ּ��йأ�
����ϲ���ּε�4�����Թ���Ϊa��b��c��d����ϲ���ּε�2�����Թ���Ϊ1��2��������¼��ֱ�Ϊ��
��a��b������a��c������a��d������a��1������a��2����
��b��c������b��d������b��1������b��2����
��c��d������c��1������c��2����
��d��1������d��2����
��1��2����
����ѡ�����������ڶ�ϲ���ּε��¼���6����
�������ΪP��A��= ![]() =0.4
=0.4
�������������ɳ��������������е����ݣ������빫ʽ���k2��ֵ������ý��ۣ������г����еĻ����¼����ùŵ�����ʹ�ʽ��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ָ������f��x����ͼ����㣨��2��4������f��3��=������ʽf��x��+f����x���� ![]() �Ľ⼯Ϊ ��
�Ľ⼯Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������� ![]() �У�
�� ![]() ����
���� ![]() ����
���� ![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ� ![]() ��
�� ![]() Ϊ
Ϊ ![]() ���е�.
���е�.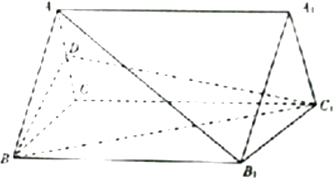
��1����֤��ֱ�� ![]() ƽ��
ƽ�� ![]() ��
��
��2�������� ![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��A��{x|��1��x��6}��B��{x|m��1��x��2m��1}����֪BA.
��1����ʵ��m��ȡֵ��Χ��
��2����x��Nʱ����A���Ӽ��ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=lnx��ax+1������aΪ��ʵ����
��1�����ۺ���f��x���ĵ����ԣ�
��2����a=1ʱ����֤��f��x����0��
��3����n��2����n��N*ʱ����֤�� ![]() ��2��
��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�ļ������У�ƽ�� ![]() ƽ��
ƽ�� ![]() ���ı���
���ı��� ![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() .
.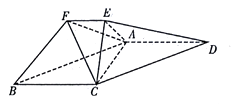
��1����֤�� ![]() ƽ��
ƽ�� ![]() ��
��
��2���� ![]() ��ƽ��
��ƽ�� ![]() �ľ��룻
�ľ��룻
��3�������� ![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����C1�ķ���Ϊ��x��2��2+y2=4��������ԭ��Ϊ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ������C2�ļ����귽��Ϊ��=2������C3�ļ����귽��Ϊ ![]() ��
��
��1��������C1��ֱ�����귽�̻�Ϊ�����귽�̣�
��2��������C3������C1��C2�ֱ��ڵ�A��B����|AB|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����Ľ����ǰ뾶Ϊ4.0 m�İ�Բ������ֻ���ڵ�·������һ����ʻ��һ����Ϊ2.7 m����Ϊ3 m�Ļ����ܲ���ʻ��������������������������Ϊa m����ôҪ����ʻ�����������������Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��A1B1C1D1���ⳤΪa��MΪBD1���е㣬N��A1C1�ϣ�������|A1N|��3|NC1|.
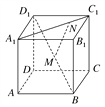
(1)��MN�ij���
(2)���жϡ�MNC����״��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com