
 (an-1),由此得出数列{an-1}是以1为首项,-
(an-1),由此得出数列{an-1}是以1为首项,- 为公比的等比数列,从而能求出数列{an}的通项公式.
为公比的等比数列,从而能求出数列{an}的通项公式. )n-1+1]-λ-n2=λ(-
)n-1+1]-λ-n2=λ(- )n-1-n2.由题意得b2n-1>b2n,可得出λ>-
)n-1-n2.由题意得b2n-1>b2n,可得出λ>- .最后结合函数的单调性可得实数λ的取值范围.
.最后结合函数的单调性可得实数λ的取值范围. an+
an+ ,则an+1-1=-
,则an+1-1=- (an-1),(4分)
(an-1),(4分) ,则
,则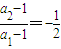 ,
, 为公比的等比数列.
为公比的等比数列. )n-1,
)n-1, )n-1+1,(6分)
)n-1+1,(6分) )n-1+1]-λ-n2=λ(-
)n-1+1]-λ-n2=λ(- )n-1-n2.
)n-1-n2. )2n-2-(2n-1)2>λ(-
)2n-2-(2n-1)2>λ(- )2n-1-(2n)2,
)2n-1-(2n)2, )2n-2[1-(-
)2n-2[1-(- )]>(2n-1)2-(2n)2,
)]>(2n-1)2-(2n)2, ,(10分)
,(10分) 对于n∈N*时单调递减,则-
对于n∈N*时单调递减,则-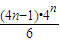 的最大值为-
的最大值为-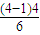 =-2,
=-2,

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com