
(
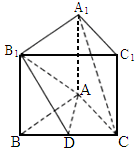
郑州四中模拟)如下图,正三棱柱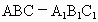 中,D是BC的中点,
中,D是BC的中点,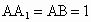 .
.
(1)
求证: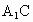 ∥平面
∥平面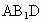 ;
;
(2)
求二面角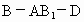 的大小;
的大小;
(3)
求点C到平面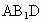 的距离.
的距离.
|
解析: (1)连接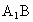 ,设 ,设 ,连结DE,∵ ,连结DE,∵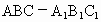 是正三棱柱且 是正三棱柱且 =AB,∴四边形 =AB,∴四边形 是正方形, 是正方形,
∴ E是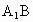 的中点, 的中点,
又 D是BC的中点,∴DE∥ . (3分) . (3分)
DE  , , 平面 平面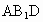 , ,
∴  ∥平面 ∥平面 . (4分) . (4分)
(2) 在平面ABC内作DF⊥AB于点F,在平面 ⊥内作FG⊥ ⊥内作FG⊥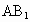 于点G,连结DG,∵平面 于点G,连结DG,∵平面 ⊥平面ABC, ⊥平面ABC,
∴ DF⊥平面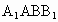 ,FG是DG在平面 ,FG是DG在平面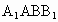 上的射影,∵FG⊥ 上的射影,∵FG⊥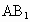 ,∴DG⊥ ,∴DG⊥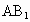 ,∴∠FGD是二面角 ,∴∠FGD是二面角 的平面角. (6分) 的平面角. (6分)
∵ 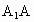 =AB=1,在正△ABC中, =AB=1,在正△ABC中, , ,
在△ ABE中, , ,
在 Rt△DFG中, , ,
∴二面角 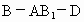 的大小为 的大小为 . (8分) . (8分)
(3) ∵平面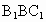 ⊥平面ABC且AD⊥BC, ⊥平面ABC且AD⊥BC,
∴ AD⊥平面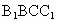 ,又AD ,又AD 平面 平面 , ,
∴平面 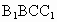 ⊥平面 ⊥平面 , ,
在平面  内作CH⊥ 内作CH⊥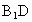 交 交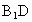 的延长线于点H,则CH的长度就是点C到平面 的延长线于点H,则CH的长度就是点C到平面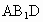 的距离.由 的距离.由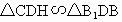 得 得
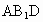 的距离是 的距离是 . (12分) . (12分) |


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:022
(2007
西安八校模拟)如下图,在△ABC中,∠ABC=∠ACB=30°,AB、AC边上的高分别为CD、BE,则以B、C为焦点,且经过D、E两点的椭圆与双曲线的离心率之和为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:044
(
莆田四中模拟)如下图,四棱锥S—ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点.(1)
求证:平面EBD⊥平面SAC;(2)
当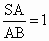 时,求二面角B—SC—D的大小.
时,求二面角B—SC—D的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com