
分析 (Ⅰ)从12个球中任取一个,记事件A=“得到红球“,事件B=“得到黄球”,事件C=“得到绿球”,事件A,B,C两两相斥,由此利用互斥事件概率加法公式能分别求出得到红球、黄球、绿球的概率.
(Ⅱ)事件“不是红球”可表示为事件“B+C”,由此利用互斥事件概率加法公式能求出得到的不是红球的概率.
解答 解:(Ⅰ)从12个球中任取一个,记事件A=“得到红球“,
事件B=“得到黄球”,事件C=“得到绿球”,
事件A,B,C两两相斥,
由题意得$\left\{\begin{array}{l}{P(A+C)=\frac{2}{3}}\\{P(A+B)=\frac{5}{12}}\\{P(A+B+C)=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{P(A)=\frac{1}{12}}\\{P(B)=\frac{1}{3}}\\{P(C)=\frac{7}{12}}\end{array}\right.$,
∴得到红球、黄球、绿球的概率分别为$\frac{1}{12},\frac{1}{3},\frac{7}{12}$.
(Ⅱ)事件“不是红球”可表示为事件“B+C”,
由(Ⅰ)及互斥事件概率加法公式得:
P(B+C)=P(B)+P(C)=$\frac{1}{3}+\frac{7}{12}=\frac{11}{12}$,
∴得到的不是红球的概率为$\frac{11}{12}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意互斥事件概率加法公式的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (-∞,4] | C. | (0,4) | D. | (0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,四边形ABCD为直角梯形,AD∥BC,AD⊥AB,AD=1,BC=2,E为CD上一点,F为BE的中点,且DE=1,EC=2,现将梯形沿BE折叠(如图2),使平面BCE⊥ABED.
如图1,四边形ABCD为直角梯形,AD∥BC,AD⊥AB,AD=1,BC=2,E为CD上一点,F为BE的中点,且DE=1,EC=2,现将梯形沿BE折叠(如图2),使平面BCE⊥ABED.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,x2+x>0 | B. | ?x>0,x2+x≤0 | C. | ?x0>0,x02+x0<0 | D. | ?x0≤0,x02+x0>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,1] | C. | (-1,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{33}{8}$ | B. | 6 | C. | 5 | D. | $\frac{69}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
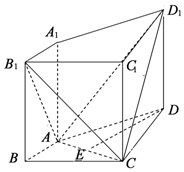 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com