
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,并按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到成绩的频率分布直方图(见下图).
分组,得到成绩的频率分布直方图(见下图).

(1)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,能否在犯错误的概率不超过0.05的前提下认为“获奖与学生的文理科有关”?
文科生 | 理科生 | 合计 | |
获奖 | 5 | ||
不获奖 | |||
合计 | 200 |
附表及公式:
![]()
![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】见解析
【解析】(1)a=[1﹣(0.01+0.015+0.03+0.015+0.005)×10]÷10=0.025,
![]() 45×0.1+55×0.15+65×0.25+75×0.3+85×0.15+95×0.05=69. …………………6分
45×0.1+55×0.15+65×0.25+75×0.3+85×0.15+95×0.05=69. …………………6分
(2)2×2列联表如下:
文科生 | 理科生 | 合计 | |
获奖 | 5 | 35 | 40 |
不获奖 | 45 | 115 | 160 |
合计 | 50 | 150 | 200 |
计算得![]() 的观测值为
的观测值为![]() ,
,
所以可以在犯错误的概率不超过0.05的前提下认为“获奖与学生的文理科有关”. ……………12分
【命题意图】本题主要考查频率分布直方图的识图,考查独立性检验知识的运用,意在考查学生的数据分析能力与应用数学知识解决实际问题的能力.


科目:高中数学 来源: 题型:
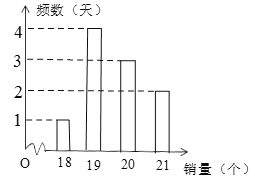
【题目】某商场对某一商品搞活动,已知该商品每一个的进价为3元,销售价为8元,每天售出的第20个及之后的半价出售.该商场统计了近10天的这种商品销量,如图所示:设![]() 为每天商品的销量,
为每天商品的销量,![]() 为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )
为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1、s2、s3,则它们的大小关系为__________.(用“>”连接)
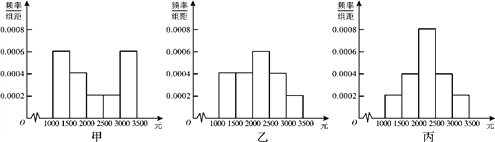
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC,已知PA⊥面ABC,AD⊥BC于D,BC=CD=AD=1,设PD=x,∠BPC=θ,记函数f(x)=tanθ,则下列表述正确的是( ) 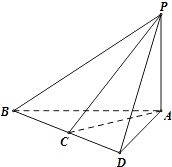
A.f(x)是关于x的增函数
B.f(x)是关于x的减函数
C.f(x)关于x先递增后递减
D.关于x先递减后递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且A,B,C成等差数列
(1)若b=2 ![]() ,c=2,求△ABC的面积;
,c=2,求△ABC的面积;
(2)若a,b,c成等比数列,试判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com