
【题目】某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了![]() 人,得到如下的统计表和频率分布直方图.
人,得到如下的统计表和频率分布直方图.
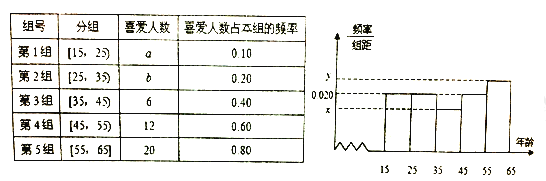
(1)写出其中![]() 及
及![]() 和
和![]() 的值;
的值;
(2)若从第1,2,3,组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求抽取的2人年龄都在![]() 的概率.
的概率.
【答案】(1)见解析(2)第1组应抽取1人,第2组应抽取2人,第3组应抽取3人.(3)![]()
【解析】试题分析:
(1)利用频率分布表可求得![]() .
. ![]() ,
, ![]() ,
, 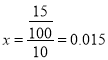 ,
, 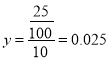
(2)利用抽样比可得第1组应抽取1人,第2组应抽取2人,第3组应抽取3人.
(3)结合(2)的结论列出所有可能的 事件,然后利用古典概型公式可得 概率值为![]() .
.
试题解析:
(Ⅰ)由表可知第3组,第4组 的人数分别为![]() ,,再根据直
,,再根据直![]() 方图可知第1组、第2组的人数也为
方图可知第1组、第2组的人数也为![]() 人,且抽样总人数
人,且抽样总人数![]() .
.
所以第5组的人数为![]() ,
,
且 ![]() ,
, ![]() ,
, ![]() ,
,
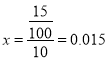 ,
, 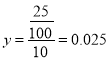
(Ⅱ)因为第1,2,3组喜欢地方戏曲的人数比![]() ,
,
那么用分层抽样的方法从这三组中抽取6人
第1组应抽取1人,
第2组应抽取2人,
第3组应抽取3人.
(Ⅲ) 由(Ⅱ)第3组抽到3人,记为![]() 第1组和第2组3人记为
第1组和第2组3人记为![]()
从这六人中随机抽取2人,所有可能结果共有15种,分别为
![]()
![]() 所抽取2人都在第3组的结果有3人,故所求的概率为
所抽取2人都在第3组的结果有3人,故所求的概率为![]()


科目:高中数学 来源: 题型:
【题目】如图所示,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F.
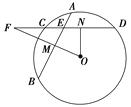
证明:(1)∠MEN+∠NOM=180°;
(2)FE·FN=FM·FO.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是正方形,
是正方形, ![]() .
.
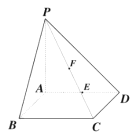
(1)求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求点![]() 、
、![]() 分别是棱
分别是棱![]() 和
和![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)=x2﹣2(a+2)x+a2 , g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max(p,q)表示p,q中的较大值,min(p,q)表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=( )
A.a2﹣2a﹣16
B.a2+2a﹣16
C.-16
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .当
.当![]() 变化时,解答下列问题:
变化时,解答下列问题:
(1)以![]() 为直径的圆能否经过点
为直径的圆能否经过点![]() ?说明理由;
?说明理由;
(2)过![]() ,
, ![]() ,
, ![]() 三点的圆在
三点的圆在![]() 轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com