
【题目】如图,某校打算在长为1千米的主干道![]() 一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域
一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域![]() (
(![]() 为直角)和以
为直角)和以![]() 为直径的半圆形区域组成,点
为直径的半圆形区域组成,点![]() (异于
(异于![]() ,
,![]() )为半圆弧上一点,点
)为半圆弧上一点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,设
,设![]() ,且
,且![]() .初步设想把咨询台安排在线段
.初步设想把咨询台安排在线段![]() ,
,![]() 上,把宣传海报悬挂在弧
上,把宣传海报悬挂在弧![]() 和线段
和线段![]() 上.
上.

(1)若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让![]() 最大,求该最大值;
最大,求该最大值;
(2)若为了让学生了解更多的省外高校,贴出更多高校的海报,打算让弧![]() 和线段
和线段![]() 的长度之和最大,求此时的
的长度之和最大,求此时的![]() 的值.
的值.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】呼和浩特市地铁一号线于2019年12月29日开始正式运营有关部门通过价格听证会,拟定地铁票价后又进行了一次调查.调查随机抽查了50人,他们的月收入情况与对地铁票价格态度如下表:
月收入(单位:百元) |
|
|
|
|
|
|
认为票价合理的人数 | 1 | 2 | 3 | 5 | 3 | 4 |
认为票价偏高的人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)若以区间的中点值作为月收入在该区间内人的人均月收入求参与调查的人员中“认为票价合理者”的月平均收入与“认为票价偏高者”的月平均收入的差是多少(结果保留2位小数);
(2)由以上统计数据填写下面![]() 列联表分析是否有
列联表分析是否有![]() 的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
月收入不低于5500元人数 | 月收入低于5500元人数 | 合计 | |
认为票价偏高者 | |||
认为票价合理者 | |||
合计 |
附:![]()
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
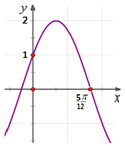
【题目】函数![]() 的部分图象如图所示,则下列叙述正确的是( )
的部分图象如图所示,则下列叙述正确的是( )
A.函数![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到
B.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C.函数![]() 在区间
在区间![]() 上是单调递增的
上是单调递增的
D.函数![]() 图象的对称中心为
图象的对称中心为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(1,0),动点M满足以MA为直径的圆与y轴相切.过A作直线x+(m﹣1)y+2m﹣5=0的垂线,垂足为B,则|MA|+|MB|的最小值为( )
A.2![]() B.2
B.2![]() C.
C.![]() D.3
D.3![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过直线y=﹣1上的动点A(a,﹣1)作抛物线y=x2的两切线AP,AQ,P,Q为切点.
(1)若切线AP,AQ的斜率分别为k1,k2,求证:k1k2为定值.
(2)求证:直线PQ过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某广告商租用了一块如图所示的半圆形封闭区域用于产品展示,该封闭区域由以![]() 为圆心的半圆及直径
为圆心的半圆及直径![]() 围成.在此区域内原有一个以
围成.在此区域内原有一个以![]() 为直径、
为直径、![]() 为圆心的半圆形展示区,该广告商欲在此基础上,将其改建成一个凸四边形的展示区
为圆心的半圆形展示区,该广告商欲在此基础上,将其改建成一个凸四边形的展示区![]() ,其中
,其中![]() 、
、![]() 分别在半圆
分别在半圆![]() 与半圆
与半圆![]() 的圆弧上,且
的圆弧上,且![]() 与半圆
与半圆![]() 相切于点
相切于点![]() .已知
.已知![]() 长为40米,设
长为40米,设![]() 为
为![]() .(上述图形均视作在同一平面内)
.(上述图形均视作在同一平面内)

(1)记四边形![]() 的周长为
的周长为![]() ,求
,求![]() 的表达式;
的表达式;
(2)要使改建成的展示区![]() 的面积最大,求
的面积最大,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com