
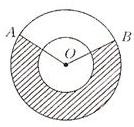
 如图所示,在同心圆中,两圆的半径分别为2,1,∠AOB=120°,则阴影部分的面积是( )
如图所示,在同心圆中,两圆的半径分别为2,1,∠AOB=120°,则阴影部分的面积是( )科目:高中数学 来源: 题型:044
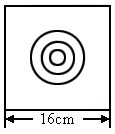
如图所示,在墙上挂着一块边长为
16cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm、4cm、6cm,某人站在3m之外向此板投镖.设投镖击中线上或没有投中木板时都不算,可重投,问:
(1)
投中大圆内的概率是多少?(2)
投中小圆与中圆形成的圆环的概率是多少?(3)
投中大圆之外的概率是多少?查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
如图所示,在墙上挂着一块边长为16cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm,4cm,6cm,某人站在3m之外向此板投镖.设投镖击中线上或没有投中木板时都不算,可重投,问:
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
如图所示,在墙上挂着一块边长为16cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm、4cm、6cm,某人站在3m之外向此板投镖.设投镖击中线上或没有投中木板时都不算,可重投,问:

(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省宁德市高级中学高一(下)期中数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com