练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    证明：cos2B-cos2A=-2sin（B+A）sin（B-A）
    考点：三角函数恒等式的证明,两角和与差的正弦函数,二倍角的余弦
    专题：推理和证明
    分析：左边=cos[A+B-（A-B）]-cos[A+B+（A-B）]，利用两角和与差的余弦，分别展开，合并同类项，即可证得右端．
    解答： 证明：左边=cos[A+B-（A-B）]-cos[A+B+（A-B）]
    =cos（A+B）cos（A-B）+sin（A+B）sin（A-B）-[cos（A+B）cos（A-B）-sin（A+B）sin（A-B）]
    =cos（A+B）cos（A-B）+sin（A+B）sin（A-B）-cos（A+B）cos（A-B）+sin（A+B）sin（A-B）
    =2sin（A+B）sin（A-B）=右边；
    所以等式成立．
    点评：本题考查三角函数恒等式的证明，考查两角和与差的余弦，考查转化思想与运算推理能力，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若（x2+ax+1）6（a＞0）的展开式中x2的系数是66，则
    ∫
    a
    0
    sinxdx的值为（　　）
    A、1+cos2
    B、1-sin2
    C、1-cos2
    D、1+sin2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

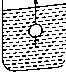    如图所示，在一个盛满水的圆柱形容器内的水面下有一个用细绳吊着的薄壁小球，小球下方有一个小孔，当慢慢地、均匀地将小球从水下面往上拉动时，圆柱形容器内水面的高度h与时间t的函数关系图象大致为（　　）
    A、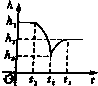
    B、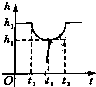
    C、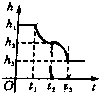
    D、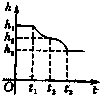

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    ，
    b
    不共线，若
    AB
    =λ1
    a
    +
    b
    ，
    AC
    =
    a
    +λ2
    b
    ，则“A、B、C三点共线”是“λ1λ2=1”的（　　）
    A、充分不必要条件
    B、必要不充分条件
    C、充分必要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给定条件p：|x+1|＞2，条件q：
    1
    3-x
    ＞1，则?q是?p的（　　）
    A、充要条件
    B、必要而不充分条件
    C、充分而不必要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    当0＜x＜1时，f（x）=x2，g（x）=x 
    1
    2
    ，h（x）=x-2，则f（x），g（x），h（x）的大小关系是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    直线l：2x+y+5=0上的点与原点的距离的最小值是（　　）
    A、2
    B、
    		5
    C、
    		10
    D、2
    		5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x，y∈R，则“x+y＞2”是“x，y中至少有一个数大于1”成立的．
    A、充分不必要条件
    B、必要不充分条件
    C、充分必要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合A={x|ln（1-x）＞0}，B={x|-1≤x≤1}，则A∩B=（　　）
    A、[-1，0]
    B、（-1，0）
    C、[-1，0）
    D、（-1，1）

    查看答案和解析>>

    同步练习册答案