
【题目】已知椭圆O: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,﹣
,﹣ ![]() ),A(x0 , y0)(x0y0≠0),其上顶点到直线
),A(x0 , y0)(x0y0≠0),其上顶点到直线 ![]() x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且
x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且 ![]() =2
=2 ![]() .
. 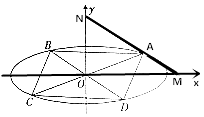
(1)证明:|MN|为定值;
(2)如图所示,若A,C关于原点对称,B,D关于原点对称,且 ![]() =λ
=λ ![]() ,求四边形ABCD面积的最大值.
,求四边形ABCD面积的最大值.
【答案】
(1)证明:其上顶点(0,b)到直线 ![]() x+y+3=0的距离为2,∴
x+y+3=0的距离为2,∴ ![]() ,解得b=1.
,解得b=1.
又椭圆O: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,﹣
,﹣ ![]() ),∴
),∴ ![]() =1,解得a2=4.
=1,解得a2=4.
∴椭圆的标准方程为: ![]() =1.
=1.
点A在椭圆上,∴ ![]() =1.
=1.
设经过点A的直线方程为:y﹣y0=k(x﹣x0),
可得M ![]() ,N(0,y0﹣kx0).
,N(0,y0﹣kx0).
∵ ![]() =2
=2 ![]() ,∴﹣x0=
,∴﹣x0= ![]() ,即k=﹣
,即k=﹣ ![]() .
.
∴|MN|= ![]() =
= ![]() =3为定值
=3为定值
(2)解:设∠AOD=α.∵ ![]() =λ
=λ ![]() ,∴2|OD|=3λ.
,∴2|OD|=3λ.
由题意可得:S四边形ABCD= ![]() =2×
=2× ![]() |OA|sinα≤3λ|OA|
|OA|sinα≤3λ|OA|
【解析】(1)其上顶点(0,b)到直线 ![]() x+y+3=0的距离为2,利用点到直线的距离公式可得
x+y+3=0的距离为2,利用点到直线的距离公式可得 ![]() ,根据椭圆O:
,根据椭圆O: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,﹣
,﹣ ![]() ),解得a2 . 可得椭圆的标准方程为:
),解得a2 . 可得椭圆的标准方程为: ![]() =1.设经过点A的直线方程为:y﹣y0=k(x﹣x0),可得M
=1.设经过点A的直线方程为:y﹣y0=k(x﹣x0),可得M ![]() ,N(0,y0﹣kx0).利用
,N(0,y0﹣kx0).利用 ![]() =2
=2 ![]() ,可得k=﹣
,可得k=﹣ ![]() .利用两点之间的距离公式可得|MN|.(2)设∠AOD=α.由
.利用两点之间的距离公式可得|MN|.(2)设∠AOD=α.由 ![]() =λ
=λ ![]() ,可得2|OD|=3λ.由题意可得:S四边形ABCD=
,可得2|OD|=3λ.由题意可得:S四边形ABCD= ![]() =2×
=2× ![]() |OA|sinα,即可得出.
|OA|sinα,即可得出.


科目:高中数学 来源: 题型:
【题目】已知等比数列 ![]() 的公比
的公比 ![]() ,且
,且 ![]() ,
, ![]() .
.
(Ⅰ)求数列 ![]() 的通项公式;
的通项公式;
(Ⅱ)设 ![]() ,
, ![]() 是数列
是数列 ![]() 的前
的前 ![]() 项和,对任意正整数
项和,对任意正整数 ![]() ,不等式
,不等式 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则2(x4﹣x1)+(x3﹣x2)的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学期末考试的语文、数学、英语、物理成绩如茎叶图所示,其中甲的一个数据记录模糊,无法辨认,用a来表示,已知两位同学期末考试四科的总分恰好相同,则甲同学四科成绩的中位数为( )
A.92
B.92.5
C.93
D.93.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示. 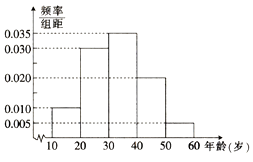
(1)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(2)若按分层抽样的方法从年龄在[20,30)以内及[40,50)以内的市民中随机抽取10人,再从这10人中随机抽取3人进行调研,记随机抽的3人中,年龄在[40,50)以内的人数为X,求X的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x20的均值和方差分别为1和8,若yi=2xi+3(i=1,2,…,20),则y1 , y2 , …,y20的均值和方差分别是( )
A.5,32
B.5,19
C.1,32
D.4,35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com