
【题目】已知函数![]() -2为自然对数的底数,
-2为自然对数的底数,![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 至多有一个公共点时,求
至多有一个公共点时,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,若函数
时,若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知以![]() 为首项的数列
为首项的数列![]() 满足:
满足: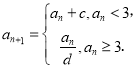
(1)当![]() ,
,![]() 时,求数列
时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() 时,试用
时,试用![]() 表示数列
表示数列![]() 前100项的和
前100项的和![]() ;
;
(3)当![]() (
(![]() 是正整数),
是正整数),![]() ,正整数
,正整数![]() 时,判断数列
时,判断数列![]() ,
,![]() ,
,![]() ,
,![]() 是否成等比数列?并说明理由.
是否成等比数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本p(x)=![]() 万元.
万元.
(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量q(m)=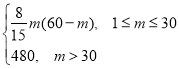 (单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
(单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且过点P
,且过点P![]() 。
。
(1)求椭圆的标准方程;
(2)已知斜率为1的直线l过椭圆的右焦点F交椭圆于A.B两点,求弦AB的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com