
分析 (Ⅰ)由题意知$A(-\sqrt{3},0),B(\sqrt{3},0)$.设点P(x,y)(y≠0),从而可得${k_{PA}}•{k_{PB}}=\frac{y}{{x+\sqrt{3}}}•\frac{y}{{x-\sqrt{3}}}=\frac{y^2}{{{x^2}-3}}$,从而解得.
(Ⅱ)假设存在实数t,使得以MN为直径的圆恒过点A;再设M(x1,y1),N(x2,y2),直线MN的方程为x=ay+t,(a∈R),联立化简可得(2a2+3)y2+4aty+2t2-6=0,从而利用韦达定理可得y1+y2=-$\frac{4at}{2{a}^{2}+3}$,y1y2=$\frac{2{t}^{2}-6}{2{a}^{2}+3}$;化简$\overrightarrow{AM}$•$\overrightarrow{AN}$=(x1+$\sqrt{3}$,y1)(x2+$\sqrt{3}$,y2)=a2y1y2+($\sqrt{3}$+t)a(y1+y2)+($\sqrt{3}$+t)2+y1y2,代入化简可得5t2+6$\sqrt{3}$t+3=0,从而解得.
解答 解:(Ⅰ)$A(-\sqrt{3},0),B(\sqrt{3},0)$.设点P(x,y)(y≠0),
则有$\frac{x^2}{3}+\frac{y^2}{2}=1$,
即${y^2}=2(1-\frac{x^2}{3})=\frac{2}{3}(3-{x^2})$,
∴${k_{PA}}•{k_{PB}}=\frac{y}{{x+\sqrt{3}}}•\frac{y}{{x-\sqrt{3}}}=\frac{y^2}{{{x^2}-3}}$=$\frac{{\frac{2}{3}(3-{x^2})}}{{{x^2}-3}}=-\frac{2}{3}$.
(Ⅱ)假设存在实数t,使得以MN为直径的圆恒过点A;
设M(x1,y1),N(x2,y2),
∵MN与x轴不重合,
∴设直线MN的方程为x=ay+t,(a∈R),
由$\left\{\begin{array}{l}{x=ay+t}\\{2{x}^{2}+3{y}^{2}-6=0}\end{array}\right.$化简得,
(2a2+3)y2+4aty+2t2-6=0,
由题意可知△>0成立,且y1+y2=-$\frac{4at}{2{a}^{2}+3}$,y1y2=$\frac{2{t}^{2}-6}{2{a}^{2}+3}$;
$\overrightarrow{AM}$•$\overrightarrow{AN}$=(x1+$\sqrt{3}$,y1)(x2+$\sqrt{3}$,y2)
=(ay1+t+$\sqrt{3}$,y1)(ay2+t+$\sqrt{3}$,y2)
=(ay1+t+$\sqrt{3}$)(ay2+t+$\sqrt{3}$)+y1y2
=a2y1y2+($\sqrt{3}$+t)a(y1+y2)+($\sqrt{3}$+t)2+y1y2
将y1+y2=-$\frac{4at}{2{a}^{2}+3}$,y1y2=$\frac{2{t}^{2}-6}{2{a}^{2}+3}$代入上式可得,
$\overrightarrow{AM}$•$\overrightarrow{AN}$=a2$\frac{2{t}^{2}-6}{2{a}^{2}+3}$-($\sqrt{3}$+t)a$\frac{4at}{2{a}^{2}+3}$+($\sqrt{3}$+t)2+$\frac{2{t}^{2}-6}{2{a}^{2}+3}$=0,
即$\frac{2{a}^{2}{t}^{2}-6{a}^{2}-4{a}^{2}t\sqrt{3}-4{a}^{2}{t}^{2}+(\sqrt{3}+t)^{2}(2{a}^{2}+3)+2{t}^{2}-6}{2{a}^{2}+3}$=0,
即a2(2t2-6-4t$\sqrt{3}$-4t2+2t2+4t$\sqrt{3}$+6)+2t2-6+3($\sqrt{3}$+t)2=0,
即5t2+6$\sqrt{3}$t+3=0,
解得,t=-$\sqrt{3}$(舍去)或t=-$\frac{\sqrt{3}}{5}$.
故t=-$\frac{\sqrt{3}}{5}$.
点评 本题考查了椭圆与直线的位置关系的判断与应用,同时考查了平面向量的应用,同时考查了学生的化简运算的能力.


科目:高中数学 来源: 题型:选择题
| A. | (a+b)2≤4ab,$a+b≤\sqrt{2{a^2}+2{b^2}}$ | B. | (a+b)2≥4ab,$a+b≤\sqrt{2{a^2}+2{b^2}}$ | ||
| C. | (a+b)2≤4ab,$a+b≥\sqrt{2{a^2}+2{b^2}}$ | D. | (a+b)2≥4ab,$a+b≥\sqrt{2{a^2}+2{b^2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
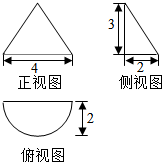
| A. | $(4+2\sqrt{13})π$ | B. | $6+(2+\sqrt{13})π$ | C. | $(\sqrt{13}+2)π$ | D. | $8+2\sqrt{13}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com