
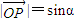 ,且
,且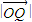 =
=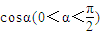 .
.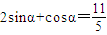 ,求tanα的值;
,求tanα的值;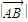 是否为定值,并说明理由;
是否为定值,并说明理由;
科目:高中数学 来源: 题型:
| 1 |
| |AD|2 |
| 1 |
| |AB|2 |
| 1 |
| |AC|2 |

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,等腰直角三角形ABC的斜边AB在![]() 轴上,原点O为AB的中点,
轴上,原点O为AB的中点,![]() ,D是OC的中点.以A、B为焦点的椭圆E经过点D.
,D是OC的中点.以A、B为焦点的椭圆E经过点D.
(1)求椭圆E的方程;
(2)过点C的直线![]() 与椭圆E相交于不同的两点M、N,点M在点C、N之间,且
与椭圆E相交于不同的两点M、N,点M在点C、N之间,且![]() ,求
,求![]() 的取值范围.
的取值范围.
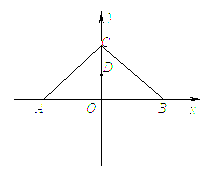
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| |AD|2 |
| 1 |
| |AB|2 |
| 1 |
| |AC|2 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年福建省厦门六中高二(下)期中数学试卷(理科)(解析版) 题型:解答题
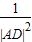 =
=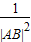 +
+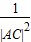 ”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出哪些结论?至少写出两个结论.
”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出哪些结论?至少写出两个结论.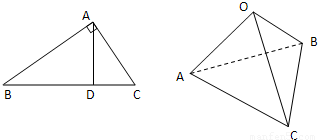
查看答案和解析>>
科目:高中数学 来源:福建省厦门六中09-10学年高二下学期期中考试(理) 题型:解答题
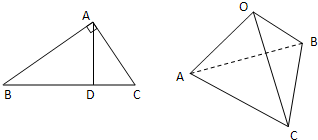
如图,在直角三角形ABC中,AD是斜边BC上的高,有很多大家熟悉的性质,例如“AB⊥AC”,勾股定理“|AB|2+|AC|2=|BC|2”和“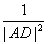 =
=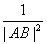 +
+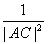 ”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
”等,由此联想,在三棱锥O-ABC中,若三条侧棱OA,OB,OC两两互相垂直,可以推出那些结论?至少写出两个结论。(本题推出一个正确的结论并给出必要的推理证明给7分,满分不超过14分)
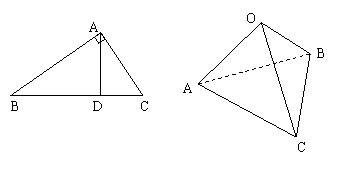 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com