分析:(1)根据A,B的范围,利用同角三角函数基本关系,利用sinA,求得cosA和tanA,进而根据tanB=tan[A-(A-B)]利用正切的两角和公式求得tanB的值,则sinB和cosB可求得.进而利用余弦的两角和公式根据cosC=-cos(A+B)求得cosC的值.
(2)根据(1)中的tanB的值,利用二倍角公式求得tan2B的值,进而利用正切的两角和公式求得tan(A+2B)的值,进而根据tanA和tanB的值判断出A,B的范围,进而求得A+2B的值.
解答:解(1)∵A,B是锐角,sinA=
∴cosA=
tanA=
∴tanB=tan[A-(A-B)]=
| tanA-tan(A-B) |
| 1+tanAtan(A-B) |
=
∴sinB=
,cosB=
又A+B+C=π
∴C=π-(A+B)
∴cosC=-cos(A+B)=-cosAcosB+sinAsinB=-
×
+
×
=-
(2)∵tanB=
∴tan2B=
=
∴tan(A+2B)=
=1
又tanA=
<1,tanB=
<1.A,B是锐角
∴0<A<
,0<B<
,∴0<A+2B<
∴A+2B=
.
点评:本题主要考查了同角三角函数的基本关系的应用.涉及了正切的二倍角公式,两角和公式等.考查了学生综合分析问题的能力.



 春雨教育同步作文系列答案
春雨教育同步作文系列答案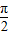 ,0<B<
,0<B<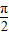 ,sinA=
,sinA=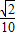 ,tan(A-B)=-
,tan(A-B)=-