
【题目】近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的分类垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1 000吨生活垃圾,数据统计如下(单位:吨):
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(1)试估计厨余垃圾投放正确的概率P;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱,“可回收物”箱,“其他垃圾”箱的投放量分别为a、b、c,其中a>0,a+b+c=600. 当数据a、b、c的方差s2最大时,写出a、b、c的值(结论不要求证明),并求出此时s2的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)80 000
;(3)80 000
【解析】
试题(1)根据古典概型概率公式求厨余垃圾投放正确的概率(2)先求对立事件概率,再根据对立事件概率关系求生活垃圾投放错误的概率;(3)先根据方差公式确定s2最大时a、b、c的值,再计算平均值,最后根据方差公式求方差
试题解析: (1)厨余垃圾投放正确的概率为
P=![]() =
=![]() =
=![]() .
.
(2)设“生活垃圾投放错误”为事件A,则事件![]() 表示“生活垃圾投放正确”.事件
表示“生活垃圾投放正确”.事件![]() 的概率为“厨余垃圾”箱里厨余垃圾量、“可回收物”箱里可回收物量与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,即P(
的概率为“厨余垃圾”箱里厨余垃圾量、“可回收物”箱里可回收物量与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,即P(![]() )=
)=![]() =
=![]() ,
,
所以P(A)=1-P(![]() )=1-
)=1-![]() =
=![]() .
.
(3)当a=600,b=0,c=0时,方差s2取得最大值.
因为![]() =
=![]() (a+b+c)=200,
(a+b+c)=200,
所以s2=![]() [(600-200)2+(0-200)2+(0-200)2]
[(600-200)2+(0-200)2+(0-200)2]
=80 000.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则 ![]() 的取值范围是( )
的取值范围是( ) 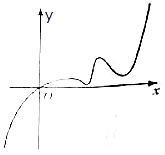
A.( ![]() ,2)
,2)
B.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
C.(2,+∞)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示(其中
的图象如图所示(其中![]() 是定义域为
是定义域为![]() 的函数
的函数![]() 的导函数),则以下说法错误的是( ).
的导函数),则以下说法错误的是( ).
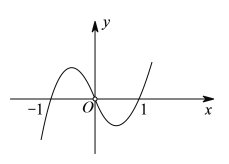
A. ![]()
B. 当![]() 时,函数
时,函数![]() 取得极大值
取得极大值
C. 方程![]() 与
与![]() 均有三个实数根
均有三个实数根
D. 当![]() 时,函数
时,函数![]() 取得极小值
取得极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)上的点到右焦点F的最小距离是
=1(a>b>0)上的点到右焦点F的最小距离是 ![]() ﹣1,F到上顶点的距离为
﹣1,F到上顶点的距离为 ![]() ,点C(m,0)是线段OF上的一个动点.
,点C(m,0)是线段OF上的一个动点.
(1)求椭圆的方程;
(2)是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点,使得( ![]() +
+ ![]() )⊥
)⊥ ![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长分别为![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、
、![]() 、…
、…![]() 的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第
的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第![]() 个、第
个、第![]() 个、……、第
个、……、第![]() 个阴影部分图形.设前
个阴影部分图形.设前![]() 个阴影部分图形的面积的平均值为
个阴影部分图形的面积的平均值为![]() .记数列
.记数列![]() 满足
满足![]() ,
,
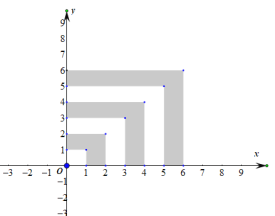
(1)求![]() 的表达式;
的表达式;
(2)写出![]() ,
,![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(3)定义![]() ,记
,记![]() ,且
,且 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]()
(1)求圆![]() 关于直线
关于直线![]() 对称的圆
对称的圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为8,求直线
截得的弦长为8,求直线![]() 的方程;
的方程;
(3)当![]() 取何值时,直线
取何值时,直线![]() 与圆
与圆![]() 相交的弦长最短,并求出最短弦长.
相交的弦长最短,并求出最短弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com