【题目】2019年是中华人民共和国成立70周年，某校党支部举办了一场“我和我的祖国”知识竞赛，满分100分，回收40份答卷，成绩均落在区间
内，将成绩绘制成如下的频率分布直方图.
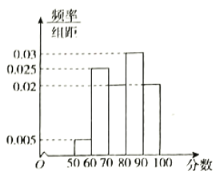
（1）估计知识竞赛成绩的中位数和平均数；
（2）从
，
分数段中，按分层抽样随机抽取5份答卷，再从对应的党员中选出3位党员参加县级交流会，求选出的3位党员中有2位成绩来自于分数段的概率.
【答案】（1）中位数为80.平均数为
（2）
【解析】
（1）由频率分布直方图可知，利用中位数和平均数的计算公式，即可求解.
（2）由频率分布直方图可知，分别求得
，
分数段中答卷数，利用列举法求得基本事件的总数，利用古典概型的概率计算公式，即可求解.
（1）由频率分布直方图可知，前3个小矩形的面积和为
，后2个小矩形的面积和为，所以估计中位数为80.
估计平均数为
.
（2）由频率分布直方图可知，分数段中答卷数分别为12，8，
抽取比例为
，所以，分数段中抽取的答卷数分别为3，2.
记中对应的3为党员为
，
，
，中对应的2为党员为
，
.
则从中选出对应的3位党员，共有不同的选法总数10种：
，
，
，
，
，
，
，
，
，
.
易知有2位来自于分数段的有3种，故所求概率为.
科目：高中数学 来源： 题型：
【题目】已知两条直线l1：y=m和l2：y= 
（m＞0），l1与函数y=|log2x|的图象从左至右相交于点A，B，l2与函数y=|log2x|的图象从左至右相交于点C，D．记线段AC和BD在X轴上的投影长度分别为a，b，当m变化时， 
的最小值为（ ）
A.16 
B.8
C.8 
D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】北京某附属中学为了改善学生的住宿条件，决定在学校附近修建学生宿舍，学校总务办公室用1000万元从政府购得一块廉价土地，该土地可以建造每层1000平方米的楼房，楼房的每平方米建筑费用与建筑高度有关，楼房每升高一层，整层楼每平方米建筑费用提高0.02万元，已知建筑第5层楼房时，每平方米建筑费用为0.8万元．
（1）若学生宿舍建筑为
层楼时，该楼房综合费用为
万元，综合费用是建筑费用与购地费用之和），写出
的表达式；
（2）为了使该楼房每平方米的平均综合费用最低，学校应把楼层建成几层？此时平均综合费用为每平方米多少万元？
【答案】（1）
；（2）学校应把楼层建成
层，此时平均综合费用为每平方米
万元
【解析】
由已知求出第
层楼房每平方米建筑费用为
万元，得到第层楼房建筑费用，由楼房每升高一层，整层楼建筑费用提高
万元
，然后利用等差数列前
项和求建筑层楼时的综合费用
；
设楼房每平方米的平均综合费用为
，则
，然后利用基本不等式求最值．
解：由建筑第5层楼房时，每平方米建筑费用为
万元，
且楼房每升高一层，整层楼每平方米建筑费用提高
万元，
可得建筑第1层楼房每平方米建筑费用为：万元．
建筑第1层楼房建筑费用为：
万元．
楼房每升高一层，整层楼建筑费用提高：
万元．
建筑第x层楼时，该楼房综合费用为：
．
；
设该楼房每平方米的平均综合费用为，
则：
，
当且仅当
，即
时，上式等号成立．
学校应把楼层建成10层，此时平均综合费用为每平方米万元．
【点睛】
本题考查简单的数学建模思想方法，训练了等差数列前n项和的求法，训练了利用基本不等式求最值，是中档题．
【题型】解答题
【结束】
20
【题目】已知
．
（1）求函数的最小正周期和对称轴方程；
（2）若
，求的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在
上的函数
满足：对任意的
，都有：
（1）求证：函数是奇函数；
（2）若当
时，有
，求证：在上是减函数；
（3）在（2）的条件下解不等式：
;
（4）在（2）的条件下求证：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个酒杯的轴截面是一条抛物线的一部分，它的方程是x2=2y，y∈[0，10]，在杯内放入一个清洁球，要求清洁球能擦净酒杯的最底部（如图），则清洁球的最大半径为 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设抛物线C：x2=2py（p＞0）的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的圆F交l于B，D两点；
（1）若∠BFD=90°，△ABD的面积为 
，求p的值及圆F的方程；
（2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
