
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC= ![]() ,M在PC上,且PA∥面BDM.
,M在PC上,且PA∥面BDM. 
(1)求直线PC与平面BDM所成角的正弦值;
(2)求平面BDM与平面PAD所成锐二面角的大小.
【答案】
(1)解:∵面PAD⊥面ABCD,△PAD为正三角形,作AD边上的高PO,
∵面PAD∩面ABCD=AD,由面面垂直的性质定理,得PO⊥面ABCD,
又ABCD是矩形,同理可得CD⊥面PAD,知CD⊥PD,
∵PC= ![]() ,PD=2,∴CD=3.
,PD=2,∴CD=3.
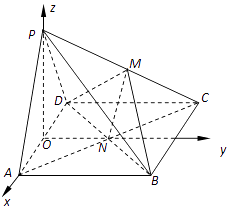
以AD中点O为坐标原点,OA所在直线为x轴,OP所在直线为z轴,AD的垂直平分线为y轴,建立如图所示的坐标系,
则P(0,0, ![]() ),A(1,0,0),B(1,3,0),C(﹣1,3,0),D(﹣1,0,0),
),A(1,0,0),B(1,3,0),C(﹣1,3,0),D(﹣1,0,0),
连结AC交BD于点N,由PA∥面MBD,面APC∩面MBD=MN,
∴MN∥PA,又N是AC的中点,
∴M是PC的中点,则M( ![]() ,
, ![]() ,
, ![]() ),
),
设面BDM的法向量为 ![]() ,
,
![]() ,
, ![]() ,
,
则 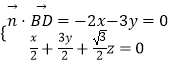 ,令x=1,解得y=﹣
,令x=1,解得y=﹣ ![]() ,z=
,z= ![]() ,得
,得 ![]() .
.
设PC与面BDM所成的角为θ,则 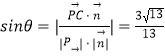 ,
,
∴直线PC与平面BDM所成角的正弦值为 ![]() .
.
(2)面PAD的法向量为向量 ![]() ,设面BDM与面PAD所成的锐二面角为φ,
,设面BDM与面PAD所成的锐二面角为φ,
则cosφ= 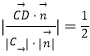 ,
,
故平面BDM与平面PAD所成锐二面角的大小为 ![]() .
.
【解析】作AD边上的高PO,由已知结合面面垂直的性质可得PO⊥面ABCD,再由ABCD是矩形,得到CD⊥PD,求解直角三角形可得CD.以AD中点O为坐标原点,OA所在直线为x轴,OP所在直线为z轴,AD的垂直平分线为y轴,建立空间直角坐标系,求出所用点的坐标,得到平面BDM的法向量 ![]() .(1)设PC与面BDM所成的角为θ,由sinθ=|
.(1)设PC与面BDM所成的角为θ,由sinθ=| ![]() 求得直线PC与平面BDM所成角的正弦值.(2)求出平面PAD的法向量
求得直线PC与平面BDM所成角的正弦值.(2)求出平面PAD的法向量 ![]() ,由两平面法向量所成角的余弦值求得平面BDM与平面PAD所成锐二面角的大小.
,由两平面法向量所成角的余弦值求得平面BDM与平面PAD所成锐二面角的大小.
【考点精析】关于本题考查的空间角的异面直线所成的角,需要了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则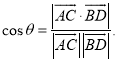 才能得出正确答案.
才能得出正确答案.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】2018年2月25日第23届冬季奥动会在韩国平昌闭幕,中国以![]() 金
金![]() 银
银![]() 铜的成绩结束本次冬奥会的征程,某校体育爱好者协会对某班进行了“本届冬奥会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),按分层抽样从该班学生中随机抽取了
铜的成绩结束本次冬奥会的征程,某校体育爱好者协会对某班进行了“本届冬奥会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),按分层抽样从该班学生中随机抽取了![]() 人,具体的调查结果如下表:
人,具体的调查结果如下表:
某班 | 满意 | 不满意 |
男生 |
|
|
女生 |
|
|
(1)若该班女生人数比男生人数多![]() 人,求该班男生人数和女生人数;
人,求该班男生人数和女生人数;
(2)若从该班调查对象的女生中随机选取![]() 人进行追踪调查,记选中的
人进行追踪调查,记选中的![]() 人中“满意”的人数为
人中“满意”的人数为![]() ,求
,求![]() 时对应事件的概率.
时对应事件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织了一次高二调研考试,考试后统计的数学成绩服从正态分布,其密度函数![]() , x∈(-∞,+∞),则下列命题不正确的是( )
, x∈(-∞,+∞),则下列命题不正确的是( )
A. 该市这次考试的数学平均成绩为80分
B. 分数在120分以上的人数与分数在60分以下的人数相同
C. 分数在110分以上的人数与分数在50分以下的人数相同
D. 该市这次考试的数学成绩标准差为10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex﹣ax2(a∈R).
(1)若函数g(x)= ![]() 是奇函数,求实数a的值;
是奇函数,求实数a的值;
(2)若对任意的实数a,函数h(x)=kx+b(k,b为实常数)的图象与函数f(x)的图象总相切于一个定点. ①求k与b的值;
②对(0,+∞)上的任意实数x1 , x2 , 都有[f(x1)﹣h(x1)][f(x2)﹣h(x2)]>0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex(x3﹣3x+3)﹣aex﹣x(x≥﹣2),若不等式f(x)≤0有解,则实数α的最小值为( )
A.![]()
B.2﹣ ![]()
C.1﹣ ![]()
D.1+2e2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴非负半轴重合,直线![]() 的极坐标方程为
的极坐标方程为![]() ,圆C的参数方程为
,圆C的参数方程为![]() ,
,
(1)求直线![]() 被圆C所截得的弦长;
被圆C所截得的弦长;
(2)已知点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆所相交于
与圆所相交于![]() 不同的两点,求
不同的两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查该校学生每周使用手机上网的时间,随机收集了若干位学生每周使用手机上网的时间的样本数据(单位:小时),将样本数据分组为![]() ,绘制了如下图所示的频率分布直方图,已知
,绘制了如下图所示的频率分布直方图,已知![]() 内的学生有5人.
内的学生有5人.

(1)求样本容量![]() ,并估计该校学生每周平均使用手机上网的时间;
,并估计该校学生每周平均使用手机上网的时间;
(2)将使用手机上网的时间在![]() 内定义为“长时间看手机”;使用手机上网的时间在
内定义为“长时间看手机”;使用手机上网的时间在![]() 内定义为“不长时间看手机”.已知在样本中有
内定义为“不长时间看手机”.已知在样本中有![]() 位学生不近视,其中“不长时间看手机”的有
位学生不近视,其中“不长时间看手机”的有![]() 位学生.请将下面的
位学生.请将下面的![]() 列联表补充完整,并判断能否在犯错误的概率不超过
列联表补充完整,并判断能否在犯错误的概率不超过![]() 的前提下认为该校学生长时间看手机与近视有关.
的前提下认为该校学生长时间看手机与近视有关.
近视 | 不近视 | 合计 | |
长时间看手机 | |||
不长时间看手机 | 15 | ||
合计 | 25 |
参考公式和数据:![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com