
【题目】已知椭圆![]() :
:![]() ,过点
,过点![]() 且与
且与![]() 轴不重合的直线与
轴不重合的直线与![]() 相交于
相交于![]() 两点,点
两点,点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)当![]() 垂直于
垂直于![]() 轴时,求直线
轴时,求直线![]() 的方程;
的方程;
(2)证明:![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)当![]() 垂直于
垂直于![]() 轴时,其方程为
轴时,其方程为![]() ,求出点
,求出点![]() 的坐标后可得直线
的坐标后可得直线![]() 的斜率,于是可得直线方程。(2)由于
的斜率,于是可得直线方程。(2)由于![]() 在
在![]() 轴上,所以只需证明点
轴上,所以只需证明点![]() 的纵坐标相等即可得到结论成立,解题时注意直线方程的设法.
的纵坐标相等即可得到结论成立,解题时注意直线方程的设法.
(1)设点![]() ,
,
当![]() 垂直于
垂直于![]() 轴时,可得
轴时,可得![]() ,所以
,所以![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,
又![]() ,
,
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
(2)法一:
①当直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() 方程为
方程为![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,因此
,因此![]() ,所以
,所以![]() .
.
若![]() ,则
,则![]() ,此时
,此时![]() 方程为
方程为![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,因此
,因此![]() ,所以
,所以![]() .
.
综上可得![]() .
.
②当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,
,
由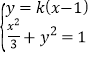 消去y整理得
消去y整理得![]() ,
,
其中![]() ,
,
设![]() ,
,![]() ,则
,则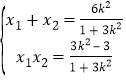 ,
,
因为![]() ,
,
所以直线![]() 的方程为
的方程为![]()
当![]() 时,得
时,得![]() ,
,
因为![]()
![]()
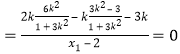 .
.
所以![]() ,
,
所以![]() .
.
法二:
设直线![]() ,
,
由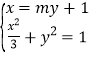 消去x整理得
消去x整理得![]() ,
,
其中![]() ,
,
设![]() ,
,![]() ,则
,则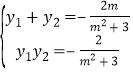 ,
,
所以![]() ,故
,故![]() 所以
所以![]() .
.
因为![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
当![]() 时,得
时,得![]() ,
,
所以![]() ,
,
所以![]() .
.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: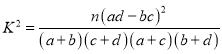 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,
中,![]() 均垂直于平面
均垂直于平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
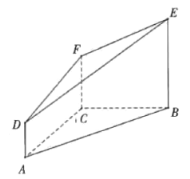
(1)过![]() 的平面
的平面![]() 与平面
与平面![]() 垂直,请在图中作出
垂直,请在图中作出![]() 截此多面体所得的截面,并说明理由;
截此多面体所得的截面,并说明理由;
(2)若![]() ,
,![]() ,求多面体
,求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的左、右焦点为
)的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .已知
.已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
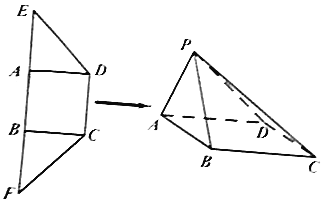
【题目】如图所示,在梯形CDEF中,四边形ABCD为正方形,且![]() ,将
,将![]() 沿着线段AD折起,同时将
沿着线段AD折起,同时将![]() 沿着线段BC折起,使得E,F两点重合为点P.
沿着线段BC折起,使得E,F两点重合为点P.
![]() 求证:平面
求证:平面![]() 平面ABCD;
平面ABCD;
![]() 求直线PB与平面PCD的所成角的正弦值.
求直线PB与平面PCD的所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏厂商对新出品的一款游戏设定了“防沉迷系统”,规则如下:
①3小时以内(含3小时)为健康时间,玩家在这段时间内获得的累积经验值![]() 单位:
单位:![]() 与游玩时间
与游玩时间![]() 小时)满足关系式:
小时)满足关系式:![]() ;
;
②3到5小时(含5小时)为疲劳时间,玩家在这段时间内获得的经验值为![]() 即累积经验值不变);
即累积经验值不变);
③超过5小时为不健康时间,累积经验值开始损失,损失的经验值与不健康时间成正比例关系,比例系数为50.
⑴当![]() 时,写出累积经验值E与游玩时间t的函数关系式
时,写出累积经验值E与游玩时间t的函数关系式![]() ,并求出游玩6小时的累积经验值;
,并求出游玩6小时的累积经验值;
⑵该游戏厂商把累积经验值E与游玩时间t的比值称为“玩家愉悦指数”,记作![]() ;若
;若![]() ,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数a的取值范围.
,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com