
ΓΨΧβΡΩΓΩά§ΜχΖ÷άύ «ΗΡ…ΤΜΖΨ≥Θ§ΫΎ‘ΦΉ ‘¥ΒΡ–¬ΨΌ¥κΘ°ΉΓΫ®≤Ω”Ύ6‘¬28»’ΡβΕ®ΝΥΑϋά®Έ“ –‘ΎΡΎΒΡ46Ηω÷ΊΒψ ‘Βψ≥« –Θ§“Σ«σ’β–©≥« –‘Ύ2020ΡξΒΉΜυ±ΨΫ®≥…ά§ΜχΖ÷άύ¥ΠάμœΒΆ≥Θ°ΈΣ¥ΥΘ§Έ“ –Ρ≥÷–―ßΕ‘―ß…ζΩΣ’ΙΝΥΓΑά§ΜχΖ÷άύΓ±”–ΙΊ÷Σ ΕΒΡΫ≤Ήυ≤ΔΫχ––≤β ‘Θ§ΫΪΥυΒΟ≤β ‘≥…Φ®’ϊάμΚσΘ§Μφ÷Τ≥ωΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΥυ ΨΘ°

Θ®1Θ©«σΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–aΒΡ÷ΒΘ§≤ΔΙάΦΤ≤β ‘ΒΡΤΫΨυ≥…Φ®ΘΜ
Θ®2Θ©ΫΪΤΒ¬ ”ΈΣœύ”ΠΒΡΗ≈¬ Θ§»γΙϊ¥”≤ΈΦ”≤β ‘ΒΡΆ§―ß÷–ΥφΜζ―Γ»Γ4ΟϊΆ§―ßΘ§’β4ΟϊΆ§―ß÷–≤β ‘≥…Φ®‘Ύ![]() ΒΡ»Υ ΐΦ«ΈΣ
ΒΡ»Υ ΐΦ«ΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΘ°
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§76.5ΘΜΘ®2Θ©Ζ÷≤ΦΝ–ΦϊΫβΈωΘ§2.
Θ§76.5ΘΜΘ®2Θ©Ζ÷≤ΦΝ–ΦϊΫβΈωΘ§2.
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”ΟΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Υυ”–ΤΒ¬ ÷°ΚΆΈΣ1Θ®Φ¥Υυ”––ΓΨΊ–ΈΟφΜΐ÷°ΚΆΈΣ1Θ©Ω…ΦΤΥψ≥ω![]() Θ§ΟΩΉι÷–ΦδΒψ÷Β≥Υ“‘ΗΟΉιΤΒ¬ œύΦ”Ω…ΒΟΙάΦΤΒΡΤΫΨυ≥…Φ®ΘΜ
Θ§ΟΩΉι÷–ΦδΒψ÷Β≥Υ“‘ΗΟΉιΤΒ¬ œύΦ”Ω…ΒΟΙάΦΤΒΡΤΫΨυ≥…Φ®ΘΜ
Θ®2Θ©”…Θ®1Θ©ΒΟ≥…Φ®‘Ύ![]() ΒΡΤΒ¬ ΈΣ
ΒΡΤΒ¬ ΈΣ![]() Θ§“ρ¥Υ”–
Θ§“ρ¥Υ”–![]() Θ§
Θ§![]() ΒΡΩ…Ρή»Γ÷ΒΈΣΘΚ0Θ§1Θ§2Θ§3Θ§4Θ§”…ΕΰœνΖ÷≤ΦΦΤΥψ≥ωΗςΗ≈¬ ΒΟΖ÷≤ΦΝ–Θ§”…ΤΎΆϊΙΪ ΫΩ…ΦΤΥψ≥ωΤΎΆϊ÷ΒΘ°
ΒΡΩ…Ρή»Γ÷ΒΈΣΘΚ0Θ§1Θ§2Θ§3Θ§4Θ§”…ΕΰœνΖ÷≤ΦΦΤΥψ≥ωΗςΗ≈¬ ΒΟΖ÷≤ΦΝ–Θ§”…ΤΎΆϊΙΪ ΫΩ…ΦΤΥψ≥ωΤΎΆϊ÷ΒΘ°
Θ®1Θ©”…Χβ“βΒΟΘΚ![]()
Υυ“‘ΘΚ![]() ,
,
ΤΫΨυ≥…Φ®ΈΣΘΚ![]() Θ°
Θ°
Θ®2Θ©“Ή÷Σ≤β ‘≥…Φ®‘Ύ![]() ΒΡΤΒ¬ ΈΣ
ΒΡΤΒ¬ ΈΣ![]()
Ι ![]() Θ°
Θ°
![]() ΒΡΩ…Ρή»Γ÷ΒΈΣΘΚ0Θ§1Θ§2Θ§3Θ§4
ΒΡΩ…Ρή»Γ÷ΒΈΣΘΚ0Θ§1Θ§2Θ§3Θ§4
![]()
![]()
![]()
![]()
![]()
![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() Θ°
Θ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ®“ε‘ΎR…œΒΡΤφΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±,
±, 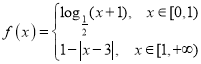
‘ρΚ· ΐ![]() ΒΡΥυ”–ΝψΒψ÷°ΚΆΈΣ_____Θ°
ΒΡΥυ”–ΝψΒψ÷°ΚΆΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() Θ§Κ· ΐ
Θ§Κ· ΐ![]()
Θ®1Θ©ΫβΙΊ”Ύ![]() ΒΡ≤ΜΒ» Ϋ
ΒΡ≤ΜΒ» Ϋ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ≤ΜΒ» Ϋ![]() Ε‘»Έ“β Β ΐ
Ε‘»Έ“β Β ΐ![]() Κψ≥…ΝΔΘ§«σ
Κψ≥…ΝΔΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»π Ω ΐ―ßΦ“ΓΔΈοάμ―ßΦ“≈Ζά≠ΖΔœ÷»Έ“ΜΆΙΕύΟφΧεΘ®Φ¥ΕύΟφΧεΡΎ»Έ“βΝΫΒψΒΡΝ§œΏΕΦ±ΜΆξ»ΪΑϋΚ§‘ΎΗΟΕύΟφΧε÷–Θ§÷±Ιέ…œΫ≤ «÷ΗΟΜ”–ΑΦœίΜρΩΉΕ¥ΒΡΕύΟφΧεΘ©ΒΡΕΞΒψ ΐVΓΔάβ ΐEΦΑΟφ ΐF¬ζΉψΒ» ΫV©¹E+FΘΫ2Θ§’βΗωΒ» Ϋ≥ΤΈΣ≈Ζά≠ΕύΟφΧεΙΪ ΫΘ§±Μ»œΈΣ « ΐ―ßΝλ”ρΉνΤ·ΝΝΓΔΦρΫύΒΡΙΪ Ϋ÷°“ΜΘ§œ÷ Β…ζΜν÷–¥φ‘ΎΚήΕύΤφΟνΒΡΦΗΚΈΧεΘ§œ÷¥ζΉψ«ρΒΡΆβΙέΦ¥»ΓΉ‘“Μ÷÷≤ΜΆξ»Ϊ’ΐΕύΟφΧεΘ§Υϋ «”…12ΩιΚΎ…Ϊ’ΐΈε±Ώ–ΈΟφΝœΚΆ20ΩιΑΉ…Ϊ’ΐΝυ±Ώ–ΈΟφΝœΙΙ≥…ΒΡΘ°20 άΦΆ80Ρξ¥ζΘ§Μ·―ßΦ“Ο«≥…ΙΠΒΊ“‘ΧΦ‘≠Ή”ΈΣΕΞΒψΉι≥…ΝΥΗΟ÷÷ΫαΙΙΘ§≈≈Ν–≥ω»Ϊ άΫγΉν–ΓΒΡ“ΜΩ≈ΓΑΉψ«ρΓ±Θ§≥ΤΈΣΓΑΑΆΩΥ«ρΘ®BuckyballΘ©Γ±Θ°‘ρΓΑΑΆΩΥ«ρΓ±ΒΡΕΞΒψΗω ΐΈΣΘ® Θ©

A.180B.120C.60D.30
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§![]() .
.
Θ®1Θ©Β±![]() ±Θ§«σ«ζœΏ
±Θ§«σ«ζœΏ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®2Θ©«σΚ· ΐfΘ®xΘ©ΒΡΦΪ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§![]() Θ°
Θ°
Θ®1Θ©»τ![]() .
.
Θ®ΔΓΘ©«σ«ζœΏ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®ΔΔΘ©«σΚ· ΐ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() ΡΎΒΡΦΪ¥σ÷ΒΒΡΗω ΐΘ°
ΡΎΒΡΦΪ¥σ÷ΒΒΡΗω ΐΘ°
Θ®2Θ©»τ![]() ‘Ύ
‘Ύ![]() ΡΎΒΞΒςΒίΦθΘ§«σ Β ΐ
ΡΎΒΞΒςΒίΦθΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() Θ§
Θ§![]() Θ§
Θ§![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΡΎΫ«
ΡΎΫ«![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡΕ‘±ΏΘ§»τ
ΒΡΕ‘±ΏΘ§»τ![]() Ά§ ±¬ζΉψœ¬Ν–ΥΡΗωΧθΦΰ÷–ΒΡ»ΐΗωΘΚΔΌ
Ά§ ±¬ζΉψœ¬Ν–ΥΡΗωΧθΦΰ÷–ΒΡ»ΐΗωΘΚΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜΔέ
ΘΜΔέ![]() ΘΜΔή
ΘΜΔή![]() .
.
Θ®1Θ©¬ζΉψ”–Ϋβ»ΐΫ«–ΈΒΡ–ρΚ≈ΉιΚœ”–ΡΡ–©ΘΩ
Θ®2Θ©‘ΎΘ®1Θ©Υυ”–ΉιΚœ÷–»Έ―Γ“ΜΉιΘ§≤Δ«σΕ‘”Π![]() ΒΡΟφΜΐ.
ΒΡΟφΜΐ.
Θ®»τΥυ―ΓΧθΦΰ≥ωœ÷Εύ÷÷Ω…ΡήΘ§‘ρΑ¥ΦΤΥψΒΡΒΎ“Μ÷÷Ω…ΡήΦΤΖ÷Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ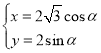 Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©.“‘Ήχ±ξ‘≠Βψ
ΈΣ≤Έ ΐΘ©.“‘Ήχ±ξ‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§![]() ÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§÷±œΏ
÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§÷±œΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() Θ§«“
Θ§«“![]() ”κ
”κ![]() ΫΜ”Ύ
ΫΜ”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ§“―÷ΣΒψ
ΝΫΒψΘ§“―÷ΣΒψ![]() ΒΡΦΪΉχ±ξΈΣ
ΒΡΦΪΉχ±ξΈΣ![]() .
.
Θ®1Θ©«σ«ζœΏ![]() ΒΡΤ’Ά®ΖΫ≥ΧΚΆ÷±œΏ
ΒΡΤ’Ά®ΖΫ≥ΧΚΆ÷±œΏ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘ§≤Δ«σ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘ§≤Δ«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©»τΨΊ–Έ![]() ΡΎΫ””Ύ«ζœΏ
ΡΎΫ””Ύ«ζœΏ![]() «“ΥΡ±Ώ”κΉχ±ξ÷αΤΫ––Θ§«σΤδ÷ή≥ΛΒΡΉν¥σ÷Β.
«“ΥΡ±Ώ”κΉχ±ξ÷αΤΫ––Θ§«σΤδ÷ή≥ΛΒΡΉν¥σ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
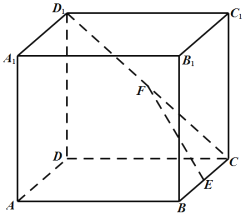
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫΧε![]() ÷–Θ§
÷–Θ§ ![]() Ζ÷±π «œΏΕΈ
Ζ÷±π «œΏΕΈ![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°
Θ®1Θ©«σ“λΟφ÷±œΏ![]() ”κ
”κ![]() Υυ≥…Ϋ«ΒΡ¥σ–ΓΘΜ
Υυ≥…Ϋ«ΒΡ¥σ–ΓΘΜ
Θ®2Θ©«σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ¥σ–ΓΘ°
Υυ≥…Ϋ«ΒΡ¥σ–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com