
分析 (1)利用函数单调性的定义,按照取值、作差、变形并判断符号、下结论的方法完成证明;
(2)这是一个不等式恒成立问题,可以转化为函数的最值问题求解,在求解之前可以先将字母a分离出来,然后构造函数,研究单调性,求其最值.
解答 解:(1)当$a=\frac{1}{2}$时,$f(x)=\frac{{x}^{2}+3x+1}{x}=x+\frac{1}{x}+3$,该函数在(2,+∞)上单调递增.
由题意设2≤x1<x2,则f(x2)-f(x1)=${x}_{2}-{x}_{1}+\frac{1}{{x}_{2}}-\frac{1}{{x}_{1}}$
=$({x}_{2}-{x}_{1})(\frac{{x}_{1}{x}_{2}-1}{{x}_{1}{x}_{2}})$①
因为2≤x1<x2,所以x2-x1>0,x1x2>0,x1x2-1>0,
所以①式>0,即f(x2)-f(x1)>0,
所以f(x2)>f(x1),故函数f(x)在[2,+∞)上单调递增.
(2)由f(x)>0有$\frac{{x}^{2}+3x+2a}{x}>0$对x∈[2,+∞)恒成立,
即2a>-x2-3x对x∈[2,+∞)恒成立,
令g(x)=-x2-3x,x∈[2.+∞),
该二次函数在$(-\frac{3}{2},+∞)$上递减,所以该函数在[2,+∞)上递减,
故g(x)max=g(2)=-10.
所以要使原式成立,只需2a>g(x)max=-10成立,
即a>-5即为所求.
点评 对于函数的单调性,一般采用定义法或导数法进行判断或求解,本题用的是定义法;而不等式恒成立问题,一般转化为函数的最值解决问题,能分离参数的尽量分离参数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,1) | C. | (0,$\frac{1}{2}$) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
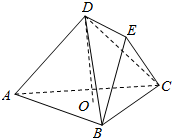 如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.
如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{PC}$和$\overrightarrow{BD}$ | B. | $\overrightarrow{DA}$和$\overrightarrow{PB}$ | C. | $\overrightarrow{PD}$与$\overrightarrow{AB}$ | D. | $\overrightarrow{PC}$与$\overrightarrow{AD}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com