(本小题共l4分)
已知

函数
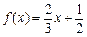
,
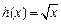
.
(Ⅰ)设函数
F(
x)=18
f(
x)-
x2[
h(
x)]
2,求
F(
x)的单调区间与极值;
(Ⅱ)设
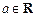
,解关于
x的方程
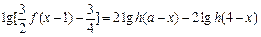
;
(Ⅲ)设
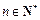
,证明:
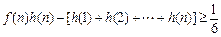
.
解:(Ⅰ)
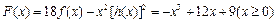
,
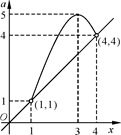
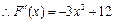
.
令
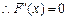
,得
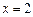
(
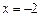
舍去).
当
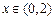
时.
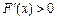
;当

时,
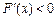
,
故当
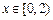
时,
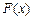
为增函数;当
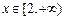
时,
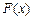
为减函数.
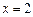
为
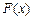
的极大值点,且
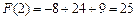
.
(Ⅱ)方法一:原方程可化为
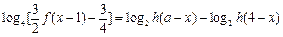
,
即为
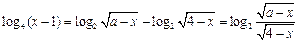
,且
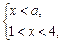
①当
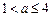
时,
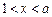
,则
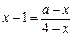
,即
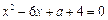
,
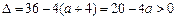
,此时
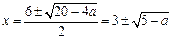
,∵
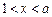
,
此时方程仅有一解
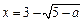
.
②当
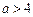
时,
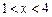
,由
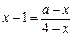
,得
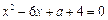
,
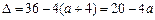
,
若
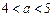
,则
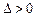
,方程有两解
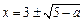
;
若
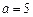
时,则

,方程有一解
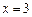
;
若
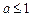
或
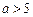
,原方程无解.
方法二:原方程可化为
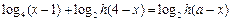
,
即
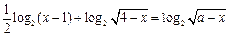
,
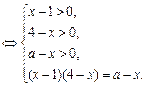
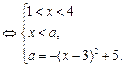
①当
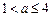
时,原方程有一解
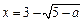
;
②当
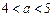
时,原方程有二解
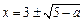
;
③当
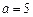
时,原方程有一解
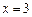
;
④当
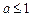
或
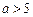
时,原方程无解.
(Ⅲ)由已知得
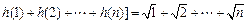
,
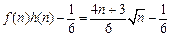
.
设数列
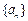
的前
n项和为
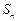
,且
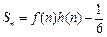
(
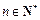
)
从而有
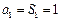
,当
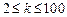
时,
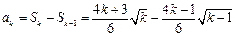
.
又
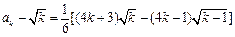
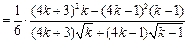
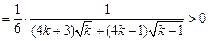
.
即对任意
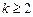
时,有
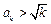
,又因为
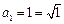
,所以
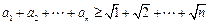
.
则
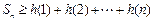
,故原不等式成立.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知
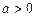
,设函数
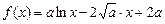
,
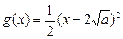
.
(Ⅰ)求函数
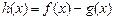
的最大值;
(Ⅱ)若
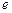
是自然对数的底数,当
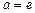
时,是否存在常数
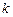
、
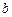
,使得不等式
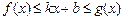
对于任意的正实数
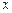
都成立?若存在,求出
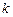
、
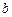
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
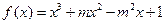
(m为常数,且m>0)有极大值9.
(1)求m的值;
(2)若斜率为-5的直线是曲线
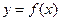
的切线,求此直线方程
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
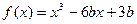
在(0,1)内有极小值,则实数
b的取值范围是
| A.(0,1) | B.(-∞,1) |
| C.(0,+∞) | D.(0,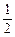 ) ) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
设
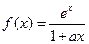
,其中
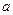
为正实数
(Ⅰ)当
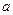
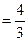
时,求
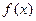
的极值点;
(Ⅱ)若
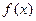
为
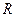
上的单调函数,求
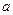
的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
曲线
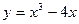
在点
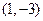
处的切线倾斜角为__________
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
曲线
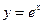
在点A(0,1)处的切线斜率为( )
| A.1 | B.2 | C.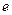 | D.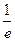 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知直线
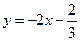
与曲线
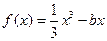
相切。
(1)求b的值;
(2)若方程
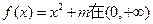
上有两个解
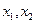
,求m的取值范围。
查看答案和解析>>

 函数
函数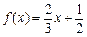 ,
,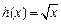 .
.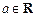 ,解关于x的方程
,解关于x的方程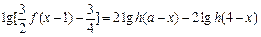 ;
;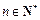 ,证明:
,证明: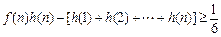 .
.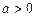 ,设函数
,设函数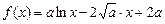 ,
,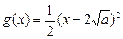 .
.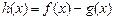 的最大值;
的最大值;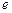 是自然对数的底数,当
是自然对数的底数,当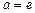 时,是否存在常数
时,是否存在常数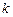 、
、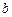 ,使得不等式
,使得不等式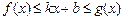 对于任意的正实数
对于任意的正实数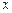 都成立?若存在,求出
都成立?若存在,求出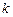 、
、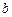 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.