
【题目】已知二次函数g(x)=ax2+c(a,c∈R),g(1)=1且不等式g(x)≤x2﹣x+1对一切实数x恒成立.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)在(Ⅰ)的条件下,设函数h(x)=2g(x)﹣2,关于x的不等式h(x﹣1)+4h(m)≤h(![]() )﹣4m2h(x),在x∈[
)﹣4m2h(x),在x∈[![]() ,+∞)有解,求实数m的取值范围.
,+∞)有解,求实数m的取值范围.
【答案】(Ⅰ)g(x)![]() ;(Ⅱ)[
;(Ⅱ)[![]() ,0)∪(0,
,0)∪(0,![]() ]
]
【解析】
(Ⅰ)先将g(1)=1代入得a+c=1,再由g(x)≤x2﹣x+1对一切实数x恒成立转化为
(a﹣1)x2+x+c﹣1≤0对一切实数x恒成立,分类讨论即可求解;
(Ⅱ)先将不等式作变形处理,可得![]() 4m2≥1
4m2≥1![]() . 在x∈[
. 在x∈[![]() ,+∞)有解,即等价于
,+∞)有解,即等价于![]() 4m2≥(1
4m2≥(1![]() )min,设y=1
)min,设y=1![]() ,求得
,求得![]() 的最小值,再解关于
的最小值,再解关于![]() 的不等式即可;
的不等式即可;
(Ⅰ)∵二次函数g(x)=ax2+c(a,c∈R),g(1)=1;∴a+c=1①;
又∵不等式g(x)≤x2﹣x+1对一切实数x恒成立;∴(a﹣1)x2+x+c﹣1≤0对一切实数x恒成立;
当a﹣1=0时,x+c﹣1≤0不恒成立,∴a=1不合题意,舍去;
当a﹣1≠0时,要使得(a﹣1)x2+x+c﹣1≤0对一切实数x恒成立,
需要满足: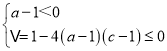 ;②,∴由①②解得a
;②,∴由①②解得a![]() ,c
,c![]() ;
;
故函数g(x)的解析式为:g(x)![]() .
.
(Ⅱ)把g(x)![]() 代入函数h(x)=2g(x)﹣2;得h(x)=x2﹣1;
代入函数h(x)=2g(x)﹣2;得h(x)=x2﹣1;
则关于x的不等式h(x﹣1)+4h(m)≤h(![]() )﹣4m2h(x)在x∈[
)﹣4m2h(x)在x∈[![]() ,+∞)有解,
,+∞)有解,
得,![]() 4m2≥1
4m2≥1![]() . 在x∈[
. 在x∈[![]() ,+∞)有解;
,+∞)有解;
只要使得![]() 4m2≥(1
4m2≥(1![]() )min;设y=1
)min;设y=1![]() ,x∈[
,x∈[![]() ,+∞),
,+∞),
则y=﹣3(![]() )2
)2![]() ,(0,
,(0,![]() ],∴当
],∴当![]() 时,ymin
时,ymin![]() ;所以,
;所以,![]() 4m2
4m2![]() ,
,
解得0<m2![]() ;∴
;∴![]() m<0或0<m
m<0或0<m![]() ;
;
故实数m的取值范围为[![]() ,0)∪(0,
,0)∪(0,![]() ].
].


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 上除顶点外的任意一点,直线
上除顶点外的任意一点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本![]() (万元)可以看成月产量
(万元)可以看成月产量![]() (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本![]() (万元)关于月产量
(万元)关于月产量![]() (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m∈R,命题p:对任意x∈[0,1],不等式x2﹣2x﹣1≥m2﹣3m恒成立,命题q:存在x∈[﹣1,1],使得m≤2x﹣1;
(Ⅰ)若命题p为真命题,求m的取值范围;
(Ⅱ)若命題q为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若![]() q是
q是![]() p的必要不充分条件,求实数a的取值范围.
p的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与
的普通方程与![]() 的直角坐标方程;
的直角坐标方程;
(2)判断曲线![]() 是否相交,若相交,求出相交弦长.
是否相交,若相交,求出相交弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的方程为
的方程为![]() ,其焦点为
,其焦点为![]() ,
,![]() 为过焦点
为过焦点![]() 的抛物线
的抛物线![]() 的弦,过
的弦,过![]() 分别作抛物线的切线
分别作抛物线的切线![]() ,设
,设![]() 相交于点
相交于点![]() .
.
(1)求![]() 的值;
的值;
(2)如果圆![]() 的方程为
的方程为![]() ,且点
,且点![]() 在圆
在圆![]() 内部,设直线
内部,设直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗器械公司在全国共有![]() 个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这
个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这![]() 个销售点的年销量绘制出如下的频率分布直方图.
个销售点的年销量绘制出如下的频率分布直方图.
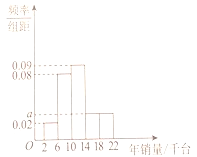
(1)完成年销售任务的销售点有多少个?
(2)若用分层抽样的方法从这![]() 个销售点中抽取容量为
个销售点中抽取容量为![]() 的样本,求该五组
的样本,求该五组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:千台)中每组分别应抽取的销售点数量.
,(单位:千台)中每组分别应抽取的销售点数量.
(3)在(2)的条件下,从该样本中完成年销售任务的销售点中随机选取![]() 个,求这两个销售点不在同一组的概率.
个,求这两个销售点不在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com